De Pillis chemotherapy model
| De Pillis chemotherapy model | |
|---|---|
| State dimension: | 1 |
| Differential states: | 6 |
| Continuous control functions: | 3 |
The model by de Pillis combines chemotherapy with immunotherapy.
Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) and
and 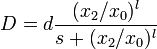 the optimal control problem is given by
the optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, u} & p_0 x_0(t_f) & + & \int_{t_0}^{t_f} p_1 x_0(t)^2 \mbox{d}t + \sum_{i=0}^{3} \int_{t_0}^{t_f} p_{i+2} u_i(t)^2 \mbox{d}t \\[1.5ex]
\mbox{s.t.} & \dot{x}_0 & = & a x_0 (1-b x_0) -c x_1 x_0 - D x_0 - K_T (1- \mbox{e}^{- x_4}) x_0 ,\\
& \dot{x}_1 & = & e x_3 - f x_1 + g \frac{x_0^2}{h+x_0^2}-p x_1 x_0 - K_N (1- \mbox{e}^{- x_4}) x_1, \\
& \dot{x}_2 & = & -m x_2 + j \frac{D^2 x_0^2}{k+ D^2 x_0^2} x_2 - q x_1 x_2 + (r_1 x_1 + r_2 x_3) x_0 \\
& & & - v x_1 x_2^2 - K_L (1- \mbox{e}^{- x_4}) x_2 + \frac{p_I x_2 x_5}{g_I + x_5} + u_2, \\
& \dot{x}_3 & = & \alpha - \beta x_3 - K_C (1- \mbox{e}^{- x_4}) x_3,\\
& \dot{x}_4 & = & - \gamma x_4 + u_0,\\
& \dot{x}_5 & = & - \mu_I x_5 + u_1.
\end{array}](https://mintoc.de/images/math/8/c/f/8cfa197d1b180e31c33607ae6827f40e.png)
The states 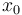 to
to 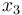 are measured in absolute cell counts, where
are measured in absolute cell counts, where 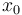 describes the number of tumor cells,
describes the number of tumor cells, 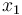 of unspecific immune cells,
of unspecific immune cells, 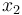 of tumor-specific cytotoxic T-cells (CD
of tumor-specific cytotoxic T-cells (CD T) and
T) and 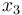 of circulating lymphocytes. The chemotherapeutic drug concentration is given by
of circulating lymphocytes. The chemotherapeutic drug concentration is given by 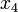 and the immunotherapeutic by
and the immunotherapeutic by 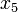 (Interleukin-2) respectively.
(Interleukin-2) respectively.
Parameters
This set of parameters can be found as “patient 9” in [].
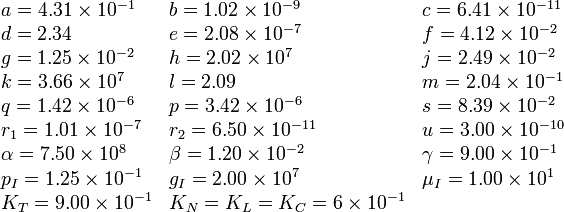
Reference Solutions
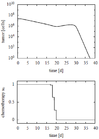
The problem can be solved with the [multiple shooting method]. For the following solutions the control functions and states are discretized on the same grid, with 100 nodes. For the objective function parameters have been chosen from the following sets to grand the results shown in the graphics below.
Objective function 1
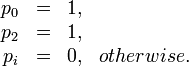
Objective function 2
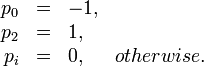
In both objective function the amount of chemotherapeutic drugs is penalized. The objective function 2 describes the worst case scenario of the tumor growth at end time.
- Reference solution plots