Difference between revisions of "Double Tank"
ClemensZeile (Talk | contribs) |
ClemensZeile (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | The | + | The double tank problem is a basic example for a switching system. It contains the dynamics of an upper and a lower tank, connected to each other with a pipe. The goal is to minimize the deviation of a certain fluid level <math>k_2</math> in the lower tank. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | lower tank | + | |
== Mathematical formulation == | == Mathematical formulation == | ||
<math> | <math> | ||
\begin{array}{ll} | \begin{array}{ll} | ||
| − | \displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T} | + | \displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T}k_1(x_2-k_2)^2 \; \text{d}t \\[1.5ex] |
\mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)}, \\[1.5ex] | \mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)}, \\[1.5ex] | ||
& \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} , \\[1.5ex] | & \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} , \\[1.5ex] | ||
| − | & \displaystyle x(0)= | + | & \displaystyle x(0)=x_0 \\[1.5ex] |
& \displaystyle \sigma \in \{1,2\},\\[1.5ex] | & \displaystyle \sigma \in \{1,2\},\\[1.5ex] | ||
& \displaystyle T=10\\ | & \displaystyle T=10\\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| + | |||
| + | with data <math>c_1=1</math> and <math>c_2=2</math>. The two states of the system correspond to the fluid levels of an upper and a lower tank. | ||
| + | The output of the upper tank flows into the lower tank, the output of the lower | ||
| + | tank exits the system, and the flow into the upper tank is restricted to either 1[lt/s] | ||
| + | or 2[lt/s]. The dynamics in each mode are then derived using Torricelli’s law, as | ||
| + | shown in Table xxx. The objective of the optimization is to have the fluid level in the | ||
| + | lower tank equal to 3[m], as reflected in the cost function in xxx | ||
| + | |||
| + | == Parameters == | ||
| + | <math>k_1=2, k_2=3, x_0=(2,2)',</math> | ||
| + | |||
| + | |||
| + | == Reference Solution == | ||
| + | By introducing the lifts <math>l_i=\sqrt{x_i}</math> , algebraically constrained as <math>l_i^2=x_i, \; l_i\geq 0,</math> the problem is easily recast with polynomial data. In this way way switch in connection with GloptiPoly3 can be applied. | ||
Revision as of 16:03, 10 December 2015
The double tank problem is a basic example for a switching system. It contains the dynamics of an upper and a lower tank, connected to each other with a pipe. The goal is to minimize the deviation of a certain fluid level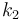 
in the lower tank.
Mathematical formulation
![\begin{array}{ll}
\displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T}k_1(x_2-k_2)^2 \; \text{d}t \\[1.5ex]
\mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)}, \\[1.5ex]
& \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} , \\[1.5ex]
& \displaystyle x(0)=x_0 \\[1.5ex]
& \displaystyle \sigma \in \{1,2\},\\[1.5ex]
& \displaystyle T=10\\
\end{array}](https://mintoc.de/images/math/4/f/8/4f8d53951df9af12f59db054262b0d8b.png)
with data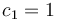 
and 
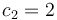. The two states of the system correspond to the fluid levels of an upper and a lower tank.
The output of the upper tank flows into the lower tank, the output of the lower
tank exits the system, and the flow into the upper tank is restricted to either 1[lt/s]
or 2[lt/s]. The dynamics in each mode are then derived using Torricelli’s law, as
shown in Table xxx. The objective of the optimization is to have the fluid level in the
lower tank equal to 3[m], as reflected in the cost function in xxx
Parameters
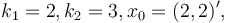
Reference Solution
By introducing the lifts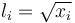 
, algebraically constrained as 
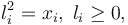the problem is easily recast with polynomial data. In this way way switch in connection with GloptiPoly3 can be applied.
