Difference between revisions of "Lotka Volterra fishing problem"

From mintOC
Jump to: navigation, search
Line 4: Line 4:
  
 
This problem was set up as a simple benchmark problem. Despite of its simple structure, the optimal solution contains a singular arcs, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.
 
This problem was set up as a simple benchmark problem. Despite of its simple structure, the optimal solution contains a singular arcs, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.
 +
 +
In this problem the Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man.
  
 
== Model dimensions and properties ==
 
== Model dimensions and properties ==
Line 13: Line 15:
 
n_x &=& 3\\
 
n_x &=& 3\\
 
n_z &=& 0\\
 
n_z &=& 0\\
−
n_u &=& 1\\
+
n_u &=& 0\\
 +
n_w &=& 1\\
 
n_p &=& 0\\
 
n_p &=& 0\\
 +
n_{\rho} &=& 0\\
 
n_c &=& 0\\
 
n_c &=& 0\\
 
n_{r^\mathrm{i}} &=& 0\\
 
n_{r^\mathrm{i}} &=& 0\\
Line 21: Line 25:
 
</math>
 
</math>
  
−
It is thus an [[ordinary differential equation|ODE]] model. The interior point equality conditions fix the initial values of the differential states.
+
It is thus an [[ordinary differential equation|ODE]] model with a single integer control function. The interior point equality conditions fix the initial values of the differential states.
  
−
== Model Equations ==
+
== Mathematical formulation ==
 +
 
 +
For <math>t \in [t_0, t_f]</math> the mixed-integer optimal control problem is given by
 +
 
 +
<math>
 +
\begin{array}{llcl}
 +
\displaystyle \min_{x, w} & x_2(t_f)  \\[1.5ex]
 +
\mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\
 +
& \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t),  \\
 +
& \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2,  \\[1.5ex]
 +
& x(0) &=& x_0, \\
 +
& w(t) &\in&  \{0, 1\}.
 +
\end{array}
 +
</math>
  
 
== Initial values and parameters ==
 
== Initial values and parameters ==
 +
 +
<math>
 +
\begin{array}{rcl}
 +
t_0 &=& 0\\
 +
t_f &=& 12\\
 +
c_0 &=& 0.4\\
 +
c_1 &=& 0.2\\
 +
x_0 &=& (0.5, 0.7, 0)^T
 +
\end{array}
 +
</math>
  
 
== Reference Solutions ==
 
== Reference Solutions ==
  
 
== Source Code ==
 
== Source Code ==
 +
 +
<code><pre>
 +
  double ref0 = 1, ref1 = 1;                /* steady state with u == 0 */
 +
 +
  rhs[0] =  xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0];
 +
  rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
 +
  rhs[2] = (xd[0]-ref0)*(xd[0]-ref0) + (xd[1]-ref1)*(xd[1]-ref1);
 +
</pre></code>
  
 
== Miscellaneous ==
 
== Miscellaneous ==

Revision as of 11:54, 29 June 2008

This problem was set up as a simple benchmark problem. Despite of its simple structure, the optimal solution contains a singular arcs, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.

In this problem the Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man.

Model dimensions and properties

The model has the following dimensions:

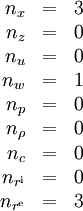
\begin{array}{rcl} n_x &=& 3\\ n_z &=& 0\\ n_u &=& 0\\ n_w &=& 1\\ n_p &=& 0\\ n_{\rho} &=& 0\\ n_c &=& 0\\ n_{r^\mathrm{i}} &=& 0\\ n_{r^\mathrm{e}} &=& 3 \end{array}

It is thus an ODE model with a single integer control function. The interior point equality conditions fix the initial values of the differential states.

Mathematical formulation

For t \in [t_0, t_f] the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\ & \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex] & x(0) &=& x_0, \\ & w(t) &\in& \{0, 1\}. \end{array}

Initial values and parameters

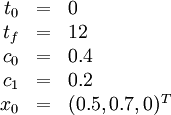
\begin{array}{rcl} t_0 &=& 0\\ t_f &=& 12\\ c_0 &=& 0.4\\ c_1 &=& 0.2\\ x_0 &=& (0.5, 0.7, 0)^T \end{array}

Reference Solutions

Source Code

  double ref0 = 1, ref1 = 1;                 /* steady state with u == 0 */

  rhs[0] =   xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0];
  rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
  rhs[2] = (xd[0]-ref0)*(xd[0]-ref0) + (xd[1]-ref1)*(xd[1]-ref1);

Miscellaneous

External references

Retrieved from "https://mintoc.de/index.php?title=Lotka_Volterra_fishing_problem&oldid=11"