Quadrotor (binary variant)
From mintOC
Revision as of 16:29, 14 October 2019 by ClemensZeile (Talk | contribs) (Created page with "{{Dimensions |nd = 1 |nx = 6 |nw = 4 |nre = 6 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... -->This site describ...")
| Quadrotor (binary variant) | |
|---|---|
| State dimension: | 1 |
| Differential states: | 6 |
| Discrete control functions: | 4 |
| Interior point equalities: | 6 |
This site describes a Quadrotor helicoptor problem variant where the continuous control is replaced via outer convexification with binary controls.
Mathematical formulation
The mixed-integer optimal control problem is given by
![\begin{array}{llclr}
\displaystyle \min_{x,u, w} & 5(x_1(t_f)-6)^2&+&5(x_3(t_f)-1)^2+(\sin(x_5(t_f)0.5))^2 +\int\limits_{t_0}^{t_f} 5( (w_2(\tau)+w_4(\tau)+w_6(\tau))^2 \ d \tau \\[1.5ex]
\mbox{s.t.}
& \dot{x}_1 & = & x_2(t), \\
& \dot{x}_2 & = & g \sin( x_5(t)) + \sum\limits_{i\in [4]}c_{1,i}w_i(t)\frac{\sin(x_5(t))}{M}, \\
& \dot{x}_3 & = & x_4(t), \\
& \dot{x}_4 & = & g \cos( x_5(t))-g+ \sum\limits_{i\in [4]}c_{1,i}w_i(t)\frac{\cos(x_5(t))}{M}, \\
& \dot{x}_5 & = & x_6(t), \\
& \dot{x}_6 & = & \sum\limits_{i\in [4]}c_{2,i}w_i(t)L \frac{1}{I} \\[1.5ex]
& x(0) &=& (0, 0, 1, 0 , 0, 0)^T, \\
& w_i(t) &\in& \{0, 1\}, i=1,\ldots,4 \\
& \sum\limits_{i=1}^{4}w_i(t) &=& 1, \\
& x_3(t) & \geq & 0, \quad t\in[t_0,t_f].
\end{array}](https://mintoc.de/images/math/c/7/3/c73ad37645d96d41b75a4d0ef176086f.png)
Parameters
These fixed values are used within the model.
![\begin{array}{rcl}
[t_0, t_f] &=& [0, 7.5],\\
(g, M, L, I) &=& (9.8, 1.3, 0.305, 0.0605),\\
c_1 &=& (0,0.001,0,0),\\
c_2 &=& (0,0,-0.001,0.001),
\end{array}](https://mintoc.de/images/math/9/e/3/9e353affa177405af782479471ad39ce.png)
Reference Solutions
If the problem is relaxed, i.e., we demand that 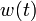 is in the continuous interval
is in the continuous interval ![[0, 1]](https://mintoc.de/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) rather than being binary, the optimal solution can be determined by means of direct optimal control.
rather than being binary, the optimal solution can be determined by means of direct optimal control.
The optimal objective value of the relaxed problem with 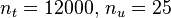 is
is 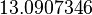 . The objective value of the solution with binary controls obtained by Combinatorial Integral Approximation (CIA) is
. The objective value of the solution with binary controls obtained by Combinatorial Integral Approximation (CIA) is 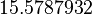 .
.
- Reference solution plots