D'Onofrio chemotherapy model

D'Onofrio chemotherapy model
State dimension:	1
Differential states:	4
Continuous control functions:	2
Path constraints:	4

This cancer chemotherapy model is based on the work of d'Onofrio. The corresponding dynamic describes the effect of two different drugs administered to the patient. An anti-angiogetic drug is used to suppress the formation of blood vessels from existing vessels and thereby starving the tumors supply of proliferating vessels. In addition a cytostatic drug effects the proliferation of the tumor cells directly. The dynamic of the problem is given by an ODE model.

Mathematical formulation

For $t \in [t_0, t_f]$ the optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, u} & x_0(t_f) &+& \alpha \int_{t_0}^{t_f} u_0(t)^2 \text{d}t \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & - \zeta x_0 \text{ln} \left( \frac{x_0}{x_1} \right) - F \; x_0 u_1, \\ & \dot{x}_1 & = & b x_0 - \mu x_1 - d x_0^{\frac{2}{3}}x_1 - G u_0 x_1 - \eta x_1 u_1, \\ & \dot{x}_2 & = & u_0, \\ & \dot{x}_3 & = & u_1, \\ [1.5ex] & u_0 & \in & [0,u_0^{max}],\\ & u_1 & \in & [0,u_1^{max}],\\ & x_2 & \leq & x_2^{max}, \\ & x_3 & \leq & x_3^{max}. \end{array}$

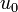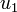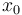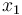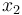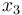where the control $u_0$ denotes the administered amount of anti-angiogetic drugs and $u_1$ the amount of cytostatic drugs. The state $x_0$ describes the volume of tumor and $x_1$ the volume of neighboring blood vessels. The remaining states $x_2$ and $x_3$ are used to constraint the maximum amount of drugs over the duration of the therapy.

Parameters

In the model these parameters are fixed.

$\begin{array}{rcl} t_0 &=& 0,\\ (\zeta, b, \mu, d, G) &=& (0.192, 5.85, 0.0, 0.00873, 0.15),\\ (x_2(0), x_3(0), u_0^{max}, x_2^{max}) &=& (0,0,75,300). \end{array}$

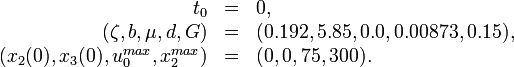
The parameters 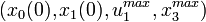$(x_0(0), x_1(0), u_1^{max}, x_3^{max})$ can be taken from the parameter sets shown in the following section. To the remaining parameters 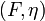$(F, \eta)$ exists no experimental data.

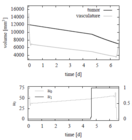
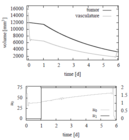
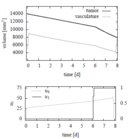
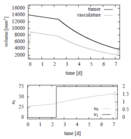
Reference Solutions

The problem can be solved with the [multiple shooting method]. For the following solutions the control functions and states are discretized on the same grid, with 100 nodes. The unknown parameters are chosen from the following parameter sets

Parameter set 1

$\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}$

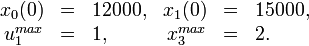
Parameter set 2

$\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}$

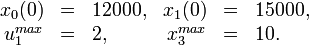
Parameter set 3

$\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}$

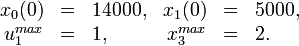
Parameter set 4

$\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}$

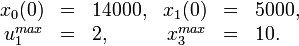
Furthermore in the objective function 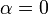$\alpha =0$ is chosen.

• Reference solution plots
• 

  Optimal controls and states computed with a multiple shooting approach on the same discretization grid with 100 nodes and parameter set 1.

• 

  Optimal controls and states with parameter set 2.

• 

  Optimal controls and states with parameter set 3.

• 

  Optimal controls and states with parameter set 4.

Variants

• a variant where partial outer convexification is applied on the control and the continous control is replaces by binary controls, see also D'Onofrio model (binary variant),

Source Code

• Muscod code at D'Onofrio chemotherapy model (Muscod)

References

There were no citations found in the article.