DOW Experimental Design
| DOW Experimental Design | |
|---|---|
| State dimension: | 1 |
| Differential states: | 11 |
| Discrete control functions: | 2 |
| Path constraints: | 4 |
| Interior point equalities: | 11 |
The DOW Experimental Design problem models the OED problem for the parameter estimation problem formulated by the DOW Chemical Co. in 1981. The following formulation is taken from [1].
Contents
[hide]Chemical background
The chemical species are disguised for proprietary reasons and the desired reaction is given by 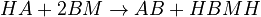 , where
, where 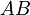 is the desired product. The reactions are described as follows:
is the desired product. The reactions are described as follows:
Slow Kinetic Reactions:

Acid-Base Reactions:
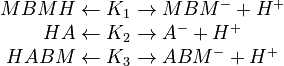
In order to devise a model to account for these reactions, it is first necessary to distinguish between the overall concentration of a species and the concentration of its neutral form. Overall concentrations are defined for three components based on neutral and ionic species
![\begin{align}
\left[HBMH\right] &= \left[ (MBMH)_N \right] + \left[ MBM^- \right] \\
\left[HA\right] &= \left[ (HA)_N \right] + \left[ A^- \right] \\
\left[HABM\right] &= \left[ (HABM)_N \right] + \left[ ABM^- \right]
\end{align}](https://mintoc.de/images/math/8/a/9/8a90809e1d9fb52552b742b87f38a098.png)
Here ![[ \ ]](https://mintoc.de/images/math/7/5/4/7541b1af090dec7db3eb1953f2b90cc1.png) denotes the concentration of the species in
denotes the concentration of the species in  .
By assuming the rapid acid-base reactions are at equilibrium, the equilibrium constants
.
By assuming the rapid acid-base reactions are at equilibrium, the equilibrium constants 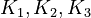 can be defined as
can be defined as
![\begin{align}
K_1 &= \frac{[MBM^-][H^+]}{[(MBMH)_N]} \\
K_2 &= \frac{[A^-][H^+]}{[(HA)_N]} \\
K_3 &= \frac{[ABM^-][H^+]}{[(HABM)_N]}
\end{align}](https://mintoc.de/images/math/0/f/c/0fc9353e835b909394feb2943063cf73.png)
The anionic species may then be represented by
![\begin{align}
\left[MBM^-\right] &= \frac{K_1[MBMH]}{K_1 + [H^+]} && \quad (a) \\
\left[A^-\right] &= \frac{K_2[HA]}{K_2 + [H^+]} && \quad (b)\\
\left[ABM^-\right] &= \frac{K_3[HABM]}{K_3 + [H^+]} && \quad (c)
\end{align}](https://mintoc.de/images/math/9/e/e/9ee28304dd2ce28499942f31c87106a4.png)
Material balance equations for the three reactants in the slow kinetic reactions yield:
![\begin{align}
\frac{d[M^-]}{dt} &= -k_1 \left[ M^- \right] \left[ BM \right] + k_{-1} \left[ MBM^- \right] - k_3 \left[ M^- \right]\left[ AB \right] + k_{-1} \left[ ABM^- \right] && \quad (d)\\
\frac{d[BM]}{dt} &= -k_1 \left[ M^- \right] \left[ BM \right] + k_{-1} \left[ MBM^- \right] - k_2 \left[ A^- \right]\left[ BM \right] && \quad (e)\\
\frac{d[AB]}{dt} &= -k_3 \left[ M^- \right] \left[ AB \right] + k_{-3} \left[ ABM^- \right] && \quad (f)
\end{align}](https://mintoc.de/images/math/6/e/7/6e7496978a48089559abb74f5d4859ac.png)
From stoichiometry, rate expressions can also be written for the total species:
![\begin{align}
\frac{d[MBMH]}{dt} &= k_1 \left[ M^- \right] \left[ BM \right] - k_{-1} \left[ MBM^- \right] && \quad (g)\\
\frac{d[HA]}{dt} &= k_2 \left[ A^- \right] \left[ BM \right] && \quad (h)\\
\frac{d[HABM]}{dt} &= k_2 \left[ A^- \right] \left[ BM \right] + k_3 \left[ M^- \right] \left[ AB \right] - k_{-3} \left[ ABM^- \right] && \quad (i)
\end{align}](https://mintoc.de/images/math/f/b/a/fbaa5e23b96608be8ee90fc5f138b1af.png)
An electroneutrality constraint gives the hydrogen ion concentration ![\left[ H^+ \right]](https://mintoc.de/images/math/a/d/0/ad0539982a2a429c51ee7e34fc22d0d4.png) as
as
![\left[ H^+ \right] + \left[ Q^+ \right] = \left[ M^- \right] + \left[ MBM^- \right] + \left[ A^- \right] + \left[ ABM^- \right] \quad \quad (j)](https://mintoc.de/images/math/a/c/7/ac79dfa07916df16abf91a7746ab38fb.png)
Based on similarities of reacting species, we assume
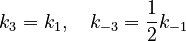
With these assumptions, the three rate constants 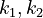 and
and 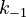 must be estimated. Each of these can be fitted with two adjustable model parameters, assuming an Arrhenius temperature dependence. That is
must be estimated. Each of these can be fitted with two adjustable model parameters, assuming an Arrhenius temperature dependence. That is
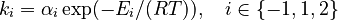
Here 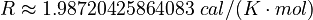 is the gas constant and
is the gas constant and 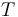 is the reaction temperature in Kelvins. The parameters
is the reaction temperature in Kelvins. The parameters 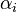 , given in
, given in 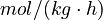 , represent the pre-exponential factors and the
, represent the pre-exponential factors and the 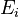 , with unit
, with unit  , are the activation energies.
, are the activation energies.
Mathematical formulation
The chemical processes  can be expressed mathematically as six differential equations and four algebraic equations:
can be expressed mathematically as six differential equations and four algebraic equations:
![\begin{align}
\dot{y}_1 &= -k_2 y_8 y_2 && \quad (1),(h) \\
\dot{y}_2 &= -k_1 y_6 y_2 + k_{-1} y_{10} - k_2 y_8 y_2 && \quad (2),(e) \\
\dot{y}_3 &= k_2 y_8 y_2 + k_1 y_6 y_4 - \frac{1}{2} k_{-1} y_9 && \quad (3),(i) \\
\dot{y}_4 &= -k_1 y_6 y_4 + \frac{1}{2} k_{-1} y_9 && \quad (4),(f) \\
\dot{y}_5 &= k_1 y_6 y_2 - k_{-1} y_{10} && \quad (5),(g) \\
\dot{y}_6 &= -k_1 (y_6 y_2 + y_6 y_4) + k_{-1} (y_{10} + \frac{1}{2} y_9) && \quad (6),(d) \\
y_7 &= -\left[ Q^+ \right] + y_6 + y_8 + y_9 + y_{10} && \quad (7),(j)\\
y_8 &= \frac{\theta_8 y_1}{\theta_8 + y_7} && \quad (8),(b)\\
y_9 &= \frac{\theta_9 y_3}{\theta_9 + y_7} && \quad (9),(c)\\
y_{10} &= \frac{\theta_7 y_5}{\theta_7 + y_7} && \quad (10),(a)
\end{align}](https://mintoc.de/images/math/c/d/8/cd8bdeab86edf9fad2f9422431b74bc0.png)
Here the letters in parentheses stand for the corresponding chemical process and the quantity ![\left[Q^+\right]=0.0131](https://mintoc.de/images/math/e/e/f/eefe4f88e9b2b92bf629a01ca55418cf.png) is a constant during the reaction.
The nine parameters form the vector
is a constant during the reaction.
The nine parameters form the vector
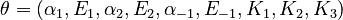
The predicted concentrations form the vector
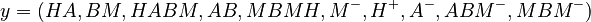
Let 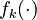 denote the right hand side of equation
denote the right hand side of equation 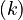 for
for 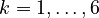 .
We reformulate the last four algebraic equations as differential ones:
.
We reformulate the last four algebraic equations as differential ones:
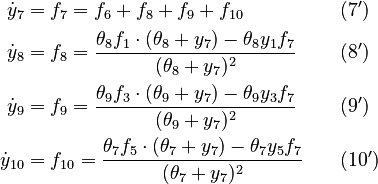
The right hand sides of  and
and 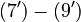 are summarized as the vector-valued function
are summarized as the vector-valued function 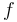 .
Moreover, let
.
Moreover, let
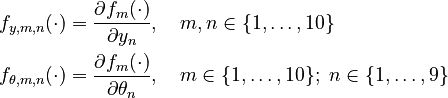
Parameters
The initial parameter estimates are:
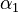 |
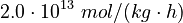 |
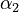 |
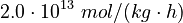 |
 |
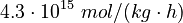 |
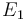 |
 |
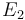 |
 |
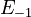 |
 |
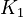 |
 |
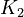 |
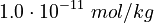 |
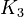 |
 |
Note that for the calculations all temperatures given in 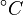 have to be rescaled to
have to be rescaled to 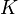 by adding
by adding  .
.
There are three datasets for different temperatures 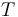 , with corresponding starting values
, with corresponding starting values
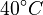 |
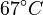 |
 |
|
|---|---|---|---|
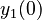 |
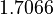 |
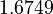 |
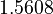 |
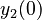 |
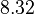 |
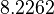 |
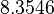 |
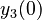 |
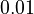 |
 |
 |
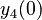 |
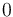 |
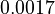 |
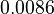 |
The initial model conditions in addition to those given in the data sets are:
![\begin{array}{l}
y_5 = 0 \\
y_6 = [Q^+] \\
y_7 = \frac{1}{2} \cdot \left( -K_2 + \sqrt{K_2^2 + 4K_2 y_1(0)} \right) \\
y_8 = y_7 \\
y_9 = 0 \\
y_{10} = 0
\end{array}](https://mintoc.de/images/math/9/c/f/9cf55186f9f0f5d6c66de068e18ebd4c.png)
To reduce the intercorrelation between the parameters in the rate constants, we apply the following reparametrization (cf. [4].):

in which 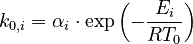 . The reference temperature in
. The reference temperature in  is chosen as the average over all performed experiments, i.e.,
is chosen as the average over all performed experiments, i.e., 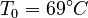 . Additionally, we add a logarithmic transformation, which gives rise to the following transformed starting values:
. Additionally, we add a logarithmic transformation, which gives rise to the following transformed starting values:
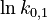 |
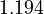 |
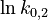 |
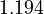 |
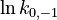 |
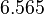 |
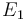 |
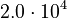 |
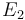 |
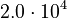 |
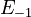 |
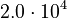 |
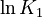 |
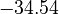 |
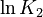 |
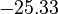 |
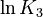 |
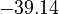 |
Optimal Experimental Design Problem
To be specified.
We are interested in when to measure (with an upper bound 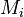 on the measuring time for each observable).
We define
on the measuring time for each observable).
We define
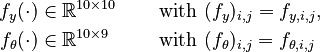
In this approach, we add the so-called sensitivities 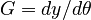 . For the differential equations this means
. For the differential equations this means

Now we formulate the OED problem as described in [2].
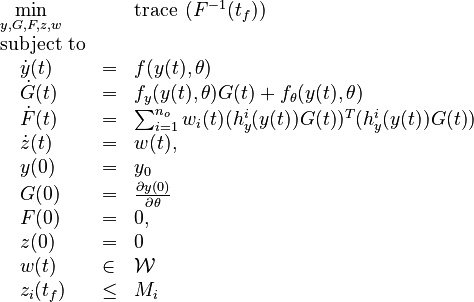
Here 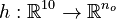 is the observed function. The
evolution of the symmetric matrix
is the observed function. The
evolution of the symmetric matrix ![F: \left[0,t_f \right] \rightarrow \mathbb{R}^{9 \times 9}](https://mintoc.de/images/math/7/1/8/718334578e24248dfbe68e385a44ec30.png) is given by the weighted sum of observability Gramians
is given by the weighted sum of observability Gramians
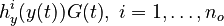 for each observed function of states. The weights
for each observed function of states. The weights 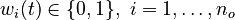 are the (binary) sampling decisions, where
are the (binary) sampling decisions, where  denotes the decision to perform a measurement at
time
denotes the decision to perform a measurement at
time 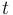 .
.
Miscellaneous and Further Reading
To be specified.
References
[1] "Nonlinear Parameter Estimation: a Case Study Comparison" by L. T. Biegler and J. J. Damiano
[2] "Optimal Experimental Design for Universal Differential Equations" by C. Plate, C.J. Martensen and S. Sager
[3] "Parameter estimation in nonlinear systems" by W.J.H. Stortelder
[4] "Parameter Estimation in Nonlinear Dynamical Systems" by Morten Rode Kristensen