Industrial robot
| Industrial robot | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Continuous control functions: | 2 |
| Path constraints: | 4 |
| Interior point equalities: | 2 |
The Industrial robot problem focuses on the KUKA LWR IV drawing a pre-defined curve on a white board, which results in a path-following problem. This means that a system should be steered along a given path while there are no constraints regarding the position at a specific time  . This concept arises often where autonomous vehicles or steering of robots are involved. The source for this problem can be found online on arXiv "Implementation of Nonlinear Model Predictive Path-Following Control for an Industrial Robot".
. This concept arises often where autonomous vehicles or steering of robots are involved. The source for this problem can be found online on arXiv "Implementation of Nonlinear Model Predictive Path-Following Control for an Industrial Robot".
Contents
[hide]Path-following problems
As the robot should follow a geometric curve but is not constrained as to when it has to be where, a path-following problem arises. The path is given by
![\mathcal{P} = \{ y \in \mathcal{R}^n: \theta \in [ \theta_0, \theta_1 ] \mapsto y = p(\theta)\}](https://mintoc.de/images/math/b/0/8/b08df6d76891dcc0db0df6356a76a742.png) where “
where “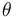 is called path parameter and
is called path parameter and 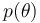 is a parametrization of
is a parametrization of 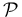 ”. The path parameter does depend on the time however the exact timing is not known beforehand but rather integrated into the optimization problem by making use of a virtual system.
”. The path parameter does depend on the time however the exact timing is not known beforehand but rather integrated into the optimization problem by making use of a virtual system.
Virtual system
A virtual system is introduced to take care of the timing of the robot. This is an additional degree of freedom which is used here as an input into an integrator. This additional optimization variable, the virtual input, 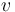 is integrated twice to produce the virtual state
is integrated twice to produce the virtual state 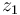 which is used as the time parameter for the path (i.e.
which is used as the time parameter for the path (i.e. 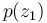 ).
).
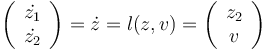
The virtual state and input are constrained by the sets 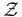 and
and 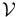 respectively.
respectively.
Model
The system for the motions of the robot are given by the function 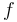 :
:
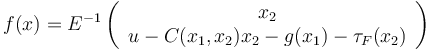
with
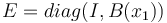
where 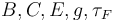 are given in the Parameters section.
are given in the Parameters section.
The objective function 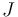 will be the integral over the so-called cost function
will be the integral over the so-called cost function 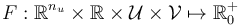 , i.e.
, i.e.
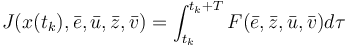 where
where 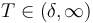 is the prediction horizon and the function
is the prediction horizon and the function 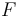 is given by
is given by 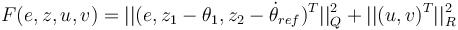 with positive semi definite matrix
with positive semi definite matrix 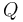 and positive definite matrix
and positive definite matrix 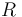 , which can be found in the original paper cited above.
, which can be found in the original paper cited above.
The path-following is introduced into the problem by optimizing the error 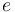 measuring the deviation of the robot from the path:
measuring the deviation of the robot from the path:
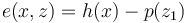
where 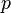 is the parametrization of
is the parametrization of 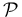 as above and
as above and 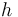 is the position of the robot given by:
is the position of the robot given by:
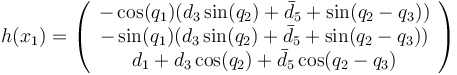
where 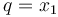 and
and 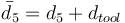 with
with 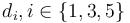 being the lengths of the links of the robot and
being the lengths of the links of the robot and 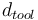 is the length of the pen and tool. These values can be found in the Parameters section as well.
is the length of the pen and tool. These values can be found in the Parameters section as well.
OCP
The optimization problem which is solved repetitively is given by
![\begin{array}{llclr}
\displaystyle \min_{\bar{u}, \bar{v}} & J &=& J(x(t_k),\bar{e}, \bar{u}, \bar{z}, \bar{v}) \\[1.5ex]
\mbox{s.t.}
& \dot{\bar{x}} & = & f(\bar{x},\bar{u}), \\
& \dot{\bar{z}} & = & l(\bar{z},\bar{v}), \\
& \bar{e} & = & h(\bar{x}) - p(\bar{z}_1), \\[1ex]
& \bar{x}(t_k) & = & x(t_k), \\
& \bar{z}(t_k) & = & z(t_k), \\[1ex]
& \bar{x} & \in & \mathcal{X}, \\
& \bar{u} & \in & \mathcal{U}, \\
& \bar{z} & \in & \mathcal{Z}, \\
& \bar{v} & \in & \mathcal{V}. \\
\end{array}](https://mintoc.de/images/math/f/9/7/f97c3b687ae027e64239822b7a145cae.png)
Parameters
The matlab script which implements the implicit formulation for 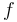 , i.e.
, i.e. 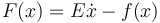 can be found on Parameters for Industrial Robot.
can be found on Parameters for Industrial Robot.
| Symbol | Value | Unit |
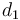
|
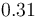
|
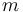
|
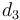
|
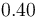
|
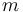
|
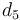
|
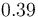
|
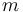
|
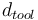
|
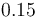
|
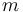
|
The Implementation Parameters for the MPFC scheme are as follows.
Reference Solutions
coming soon
References
There were no citations found in the article.
![\mathcal{X} = [-\bar{x}, \bar{x}], \text{ where } \bar{x} = (\bar{q},\bar{q},\bar{q},\bar{\dot{q}},\bar{\dot{q}},\bar{\dot{q}})^T \text{ with } \bar{q} = \infty \text{ rad}, \quad \bar{\dot{q}} = 0.5 \text{ rad/s}](https://mintoc.de/images/math/b/8/c/b8cfcb66af97f56fbcdb6964ca463714.png)
![\mathcal{U} = [-\bar{u}, \bar{u}], \text{ where } \bar{u} = (\bar{\tau},\bar{\tau},\bar{\tau})^T \text{ with } \bar{\tau} = 60 \text{ Nm}](https://mintoc.de/images/math/f/b/6/fb6244c54159a4c483384be036bd5aba.png)
![\mathcal{Z} = [\underline{z}, \bar{z}], \text{ where } \underline{z} = (0,0)^T, \bar{z} = (1750, \infty)^T](https://mintoc.de/images/math/5/0/1/501f7a5421d2b7befb77c2cb2b69e410.png)
![\mathcal{V} = [-10^4, 8 \cdot 10^3]](https://mintoc.de/images/math/3/6/0/360367a6179c00aa476c325bbd2f6c20.png)