Difference between revisions of "Cushioned Oscillation"

From mintOC
Jump to: navigation, search
(→‎Model formulation)
Line 64: Line 64:
  
  
−
The following parameters were used, to create the reference solution below, with an almost optimal final time <math> t_f = 16.66 s</math>:
+
The following parameters were used, to create the reference solution below, with an almost optimal final time <math> t_f = 8.98 s</math>:
  
−
<math> m=10, </math>
+
<math> m=5, </math>
  
 
<math> c=10, </math>
 
<math> c=10, </math>
Line 79: Line 79:
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="1">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="1">
−
  Image:Ref_sol_plot_cushioned_oscillation.png| States and Controls
+
  Image:Ref_sol_plot_cushioned_oscillation_m5.png| States and Controls
 
</gallery>
 
</gallery>
  
  
−
The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approache and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).
+
The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approach (n=80 collocation points) and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).
  
  

Revision as of 11:04, 18 January 2016

The Cushioned Oscillation is a simplified model of time optimal "stopping" of an oscillating object attached to a spring by applying a control and moving it back into the relaxed position and no velocity.

Model formulation

An object with mass 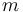m is attached to a spring with stiffness constant c .

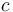If the resetting spring force is proportional to the deviation 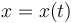x=x(t), an oscillation, induced by an external force 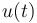u(t), satisfies:


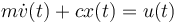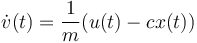m\dot v (t) + cx(t) = u(t) (which is equivalent to \dot v (t) = \frac{1}{m}(u(t) - cx(t)))


where 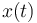x(t) denotes the deviation to the relaxed position and 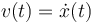v(t)=\dot x (t) the velocity of the oscillating object.


Through external force, the object has been put into an initial state :


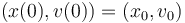
(x(0),v(0)) = (x_0,v_0)


The goal is to reset position and velocity of the object as fast as possible, meaning:


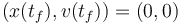(x(t_f),v(t_f)) = (0,0),


with the objective function:


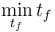
\min\limits_{t_f} t_f

Optimal Control Problem (OCP) Formulation

The above results in the following OCP


\begin{array}{llr} \min\limits_{x,v,u,t_f} & t_f\\ s.t. & \dot x (t) = v(t), & \forall t \in [0,t_f]\\ & \dot v (t)= \frac{1}{m}(u(t) - cx(t)), & \forall t \in [0,t_f]\\ \\ & x(0)=x_0,\\ & v(0)=v_0,\\ & x(t_f)=0,\\ & v(t_f)=0,\\ \\ & -u_{mm} \le u(t) \le u_{mm}, & \forall t \in [0,t_f]\\ \end{array}

Parameters and Reference Solution

The following parameters were used, to create the reference solution below, with an almost optimal final time 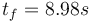t_f = 8.98 s:

m=5,

c=10,

x_0=2,

v_0=5,

u_{mm}=5


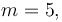
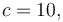
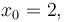
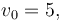
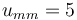
  • Reference solution plots

  • States and Controls


The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approach (n=80 collocation points) and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).



Source Code

The MATLAB script can be found in: Cushioned Oscillation (PROPT)

References

Retrieved from "https://mintoc.de/index.php?title=Cushioned_Oscillation&oldid=1272"