Difference between revisions of "Category:Sliding mode"
From mintOC
m (Initial setup of IMA paper text) |
JonasSchulze (Talk | contribs) m (Text replacement - "\<bibref\>(.*)\<\/bibref\>" to "<bib id="$1" />") |
||
| Line 1: | Line 1: | ||
| − | Solutions of model equations with [[:Category:State dependent switches | state dependent switches]] may show a sliding mode behavior in the sense of Filippov systems < | + | Solutions of model equations with [[:Category:State dependent switches | state dependent switches]] may show a sliding mode behavior in the sense of Filippov systems <bib id="Filippov1964" />. This means that at least one of the switching functions <math>\sigma_i(\cdot)</math> has infinetely many zeros on the finite time interval <math>[0, t_f]</math>. In other words, the right hand side switches infinetely often in a finite time horizon. |
== References == | == References == | ||
Revision as of 18:54, 20 January 2016
Solutions of model equations with state dependent switches may show a sliding mode behavior in the sense of Filippov systems [Filippov1964]Author: Filippov, A.F.
Journal: AMS Transl.
Pages: 199--231
Title: Differential Equations with discontinuous right hand side
Volume: 42
Year: 1964
. This means that at least one of the switching functions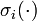 
has infinetely many zeros on the finite time interval ![[0, t_f]](https://mintoc.de/images/math/1/6/8/1681a3464dfb0673f6901981b0cd2d20.png)
. In other words, the right hand side switches infinetely often in a finite time horizon.
References
<bibreferences/>
This category currently contains no pages or media.
