Difference between revisions of "Van der Pol Oscillator (Jump)"

From mintOC
Jump to: navigation, search
 
(13 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
This is an implementation of a slightly modified form of the Van der Pol oscillator problem using [[category: Julia/JuMP || JuMP]].
+
This is an implementation of a slightly modified form of the [[Van der Pol Oscillator]] problem using [[:category: Julia/JuMP | JuMP]].
  
 
The problem in question can be stated as follows:
 
The problem in question can be stated as follows:
Line 7: Line 7:
 
\begin{array}{llclr}
 
\begin{array}{llclr}
 
  \displaystyle \max_{x, u} & x_3(t_f)  \\[1.5ex]
 
  \displaystyle \max_{x, u} & x_3(t_f)  \\[1.5ex]
−
  \mbox{s.t.} & \dot{x}_1(t) & = & (1 - x_2(t)^2) x_1(t) - x_2(t) + u(t)  \qquad & \forall t \in [t_0, t_f], \\
+
  \mbox{s.t.} & \dot{x}_1 & = & (1 - x_2^2) x_1 - x_2 + u, \\
−
  & \dot{x}_2(t) & = & x_1(t)  \qquad & \forall t \in [t_0, t_f],  \\
+
  & \dot{x}_2 & = & x_1,  \\
−
  & \dot{x}_3(t) & = & x_1(t)^2 + x_2(t)^2 + u(t)^2 \qquad & \forall t \in [t_0, t_f], \\[1.5ex]
+
  & \dot{x}_3 & = & x_1^2 + x_2^2 + u^2, \\[1.5ex]
 
  & x(0) &=& (0, 1, 0)^T, \\
 
  & x(0) &=& (0, 1, 0)^T, \\
−
  & u(t) &\in&  [-0.3, 1]  \qquad & \forall t \in [t_0, t_f].
+
  & u(t) &\in&  [-0.3, 1].
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
 
</p>
 
</p>
 
where <math> [t_0, t_f] = [0,5] </math>.
 
where <math> [t_0, t_f] = [0,5] </math>.
 +
  
 
The problem was discretized and the ODEs are solved using the explicit Euler method.
 
The problem was discretized and the ODEs are solved using the explicit Euler method.
 
Although not necessary in JuMP the code was divided into three parts (following AMPL) - model file, data file and run file. The run file calls the other files and performs additional tasks such as printing results.
 
Although not necessary in JuMP the code was divided into three parts (following AMPL) - model file, data file and run file. The run file calls the other files and performs additional tasks such as printing results.
 +
 +
A reference solution including plots done with JuMP can be found below the code!
  
  
Line 41: Line 44:
  
 
#ODE - solved with explicit euler method (i.e. x_k+1 = x_k + stepsize * f(x_k, t_k))
 
#ODE - solved with explicit euler method (i.e. x_k+1 = x_k + stepsize * f(x_k, t_k))
−
@addNLConstraint(m, ODE_nonlin[ii=1:1, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ((1 - x[2,tt]^2) * x[1,tt] - x[2,tt] + u[1,tt]) == 0)
+
@addNLConstraint(m, ODE_nonlin[ii=1:1, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ((1 - x[2,tt]^2) * x[1,tt]
 +
- x[2,tt] + u[1,tt]) == 0)
 
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  >= 0)
 
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  >= 0)
 
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  <= 0)
 
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  <= 0)
Line 109: Line 113:
 
println("Optimal objective value is: ", getObjectiveValue(m))
 
println("Optimal objective value is: ", getObjectiveValue(m))
 
println("Optimal Solution is: \n", getValue(x), getValue(u))</source>
 
println("Optimal Solution is: \n", getValue(x), getValue(u))</source>
 +
 +
== Reference solutions ==
 +
This solution was computed using JuMP with a collocation method and 300 discretization points (using the code above). The differential equations were solved using the explicit Euler Method. The optimal objective value is 2.902143.
 +
 +
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
 +
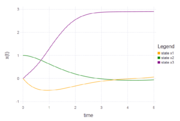
File:Vdposc states plot.PNG| Optimal states x1(t), x2(t) and x3(t).
 +
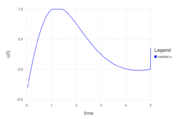
File:Vdposc control plot.PNG| Optimal control u(t).
 +
</gallery>
  
 
[[Category: Julia/JuMP]]
 
[[Category: Julia/JuMP]]

Latest revision as of 12:35, 23 February 2016

This is an implementation of a slightly modified form of the Van der Pol Oscillator problem using JuMP.

The problem in question can be stated as follows:

\begin{array}{llclr} \displaystyle \max_{x, u} & x_3(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = & (1 - x_2^2) x_1 - x_2 + u, \\ & \dot{x}_2 & = & x_1, \\ & \dot{x}_3 & = & x_1^2 + x_2^2 + u^2, \\[1.5ex] & x(0) &=& (0, 1, 0)^T, \\ & u(t) &\in& [-0.3, 1]. \end{array}

where [t_0, t_f] = [0,5] .


The problem was discretized and the ODEs are solved using the explicit Euler method. Although not necessary in JuMP the code was divided into three parts (following AMPL) - model file, data file and run file. The run file calls the other files and performs additional tasks such as printing results.

A reference solution including plots done with JuMP can be found below the code!


Model file ("vdposc_mod.jl"): 

#JuMP implementation of Van der Pol oscillator using collocation
#mod file
 
#declaring the model
m = Model(solver=IpoptSolver())
 
#defining variables
@defVar(m, x[ii=1:n_x, tt=1:N])
@defVar(m, L_control <= u[jj = 1:n_u, tt=1:N] <= U_control)
 
#set objective function
@setObjective(m, Min, x[3,N])
 
#setting constraints
#starting values
@addConstraint(m, starting_value[ii=1:n_x], x[ii,1] == x_start[ii])
 
#ODE - solved with explicit euler method (i.e. x_k+1 = x_k + stepsize * f(x_k, t_k))
@addNLConstraint(m, ODE_nonlin[ii=1:1, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ((1 - x[2,tt]^2) * x[1,tt]
 - x[2,tt] + u[1,tt]) == 0)
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  >= 0)
@addConstraint(m, ODE[ii=2:n_x, tt=1:N-1],  x[ii,tt+1] - x[ii,tt] - step_size * ode_rhs(time_disc[tt], x[:,tt], u[:,tt])[ii]  <= 0)

Data file ("vdposc_dat.jl"): 

#JuMP implementation of Van der Pol oscillator using collocation
#dat file
 
#number of states
n_x = 3;
 
#number of controls
n_u = 1;
 
##discretization
#number of shooting intervals / discretization points
N = 300;
#starting / end time
t_start = 0;
t_end = 5;
#time discretization
time_disc = linspace(t_start,t_end, N+1);
step_size = (t_end - t_start)/N;
 
#starting value
x_start = [0, 1, 0];
 
#bounds for control
L_control = -0.3;
U_control = 1;
 
 
##right hand side of ODE
function ode_rhs(time, state, control)
#give in form f1, f2, f3,...
0,
state[1],
state[1]^2 + state[2]^2 + control[1]^2
end

Run file ("vdposc_run.jl"): 

#JuMP implementation of Van der Pol oscillator using collocation
#run file
 
using JuMP;
using Ipopt;
 
 
println("----------------------------------------------------")
println("Time used for data")
@time include("vdposc_dat.jl")
println("----------------------------------------------------")
println("Time used for modeling")
@time include("vdposc_mod.jl")
println("----------------------------------------------------")
println("Time used for solving")
@time solve(m);
 
println("----------------------------------------------------")
println("----------------------------------------------------")
 
 
println("Optimal objective value is: ", getObjectiveValue(m))
println("Optimal Solution is: \n", getValue(x), getValue(u))

Reference solutions

This solution was computed using JuMP with a collocation method and 300 discretization points (using the code above). The differential equations were solved using the explicit Euler Method. The optimal objective value is 2.902143.

  • Reference solution plots

  • Optimal states x1(t), x2(t) and x3(t).

  • Optimal control u(t).

Retrieved from "https://mintoc.de/index.php?title=Van_der_Pol_Oscillator_(Jump)&oldid=1734"