Difference between revisions of "Cushioned Oscillation"

From mintOC
Jump to: navigation, search
 
(17 intermediate revisions by 3 users not shown)
Line 1: Line 1:
−
The Cushioned Oscillation is a simplified model of time optimal "stopping" of an oscillating object attached to a spring by applying a control and moving it back into the relaxed position and no velocity.
+
{{Dimensions
 +
|nd        = 1
 +
|nx        = 2
 +
|nu        = 1
 +
|nc        = 2
 +
|nre      = 4
 +
}}The Cushioned Oscillation is a simplified model of time optimal "stopping" of an oscillating object attached to a spring by applying a control and moving it back into the relaxed position and zero velocity.
  
 
== Model formulation ==  
 
== Model formulation ==  
Line 5: Line 11:
 
An object with mass <math> m </math> is attached to a spring with stiffness constant <math> c </math>.
 
An object with mass <math> m </math> is attached to a spring with stiffness constant <math> c </math>.
  
−
If the resetting spring force is proportional to the deviation <math>x=x(t)</math>, an oscillation induced by an external force <math>u(t)</math> satisfies:
+
If the resetting spring force is proportional to the deviation <math>x=x(t)</math>, an oscillation, induced by an external force <math>u(t)</math>, satisfies:
  
  
Line 12: Line 18:
  
 
where <math>x(t)</math> denotes the deviation to the relaxed position and <math> v(t)=\dot x (t) </math> the velocity of the oscillating object.
 
where <math>x(t)</math> denotes the deviation to the relaxed position and <math> v(t)=\dot x (t) </math> the velocity of the oscillating object.
−
 
−
 
  
 
Through external force, the object has been put into an initial state :
 
Through external force, the object has been put into an initial state :
−
 
  
 
<math>(x(0),v(0)) = (x_0,v_0)</math>
 
<math>(x(0),v(0)) = (x_0,v_0)</math>
−
 
  
 
The goal is to reset position and velocity of the object as fast as possible, meaning:
 
The goal is to reset position and velocity of the object as fast as possible, meaning:
−
 
  
 
<math>(x(t_f),v(t_f)) = (0,0)</math>,
 
<math>(x(t_f),v(t_f)) = (0,0)</math>,
−
 
−
 
  
 
with the objective function:
 
with the objective function:
−
 
  
 
<math>\min\limits_{t_f} t_f</math>
 
<math>\min\limits_{t_f} t_f</math>
  
−
 
+
== Optimal Control Problem Formulation ==
−
== Optimal Control Problem (OCP) Formulation ==
+
  
 
The above results in the following OCP  
 
The above results in the following OCP  
  
 +
<math> \begin{array}{llll}
  
−
<math> \begin{array}{llr}
+
\min\limits_{x,v,u,t_f}  & t_f & & \\  
−
\min\limits_{x,v,u,t_f}  & t_f\\  
+
  
−
s.t. & \dot x (t) = v(t), & \forall t \in [0,t_f]\\
+
s.t. & \dot x & = v,\\
  
−
& \dot v (t)= \frac{1}{m}(u(t) - cx(t)),  & \forall t \in [0,t_f]\\
+
& \dot v & =   \frac{1}{m}(u - c \cdot x),\\
 
\\
 
\\
−
                                                   
+
& x(0) & = x_0,\\
−
& x(0)=x_0,\\
+
& v(0) & = v_0,\\
−
 
+
& x(t_f) & = 0,\\
−
& v(0)=v_0,\\
+
& v(t_f) & = 0,\\
−
 
+
& |u| & \le u_{mm}.\\
−
& x(t_f)=0,\\
+
−
 
+
−
& v(t_f)=0,\\
+
−
 
+
−
\\
+
−
& -u_{mm} \le u(t) \le u_{mm},  & \forall t \in [0,t_f]\\
+
−
 
+
−
 
+
 
 
 
  \end{array}</math>
 
  \end{array}</math>
Line 64: Line 53:
 
== Parameters and Reference Solution ==
 
== Parameters and Reference Solution ==
  
 +
The following parameters were used, to create the reference solution below, with an almost optimal final time <math> t_f = 8.98 s</math>:
  
−
The following parameters were used, to create the reference solution below, with an almost optimal final time <math> t_f = 16.66 s</math>:
+
<math> m=5, </math>
−
 
+
−
<math> m=10, </math>
+
−
 
+
 
<math> c=10, </math>
 
<math> c=10, </math>
−
 
 
<math> x_0=2, </math>
 
<math> x_0=2, </math>
−
 
 
<math> v_0=5, </math>
 
<math> v_0=5, </math>
 +
<math> u_{mm}=5.</math>
  
−
<math> u_{mm}=5</math>
+
== Reference Solution ==
−
 
+
−
 
+
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="1">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="1">
−
  Image:Ref_sol_plot_cushioned_oscillation.png| States and Controls
+
  Image:Ref_sol_plot_cushioned_oscillation_m5.png| States and Controls
 
</gallery>
 
</gallery>
  
−
 
+
The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approach (n=80 collocation points) and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).
−
The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approache and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).
+
−
 
+
−
 
+
−
 
+
  
 
== Source Code ==
 
== Source Code ==
  
−
The MATLAB script can be found in:
+
* A MATLAB script using [[:Category:TomDyn/PROPT | PROPT]] can be found in: [[Cushioned Oscillation (PROPT)]]
−
 
+
−
[[Category:TomDyn/PROPT]] [[Cushioned Oscillation]]
+
  
 
== References ==
 
== References ==
  
−
[[Category:MIOCP]]
+
[[Category:MIOCP]]
 +
[[Category:Bang bang]]
 +
[[Category:ODE model]]
 +
[[Category: Minimum time]]

Latest revision as of 10:06, 30 June 2016

Cushioned Oscillation
State dimension: 1
Differential states: 2
Continuous control functions: 1
Path constraints: 2
Interior point equalities: 4

The Cushioned Oscillation is a simplified model of time optimal "stopping" of an oscillating object attached to a spring by applying a control and moving it back into the relaxed position and zero velocity.

Model formulation

An object with mass 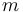m is attached to a spring with stiffness constant c .

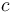If the resetting spring force is proportional to the deviation 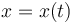x=x(t), an oscillation, induced by an external force 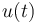u(t), satisfies:


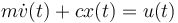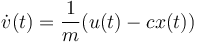m\dot v (t) + cx(t) = u(t) (which is equivalent to \dot v (t) = \frac{1}{m}(u(t) - cx(t)))


where 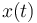x(t) denotes the deviation to the relaxed position and 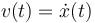v(t)=\dot x (t) the velocity of the oscillating object.

Through external force, the object has been put into an initial state :

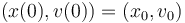
(x(0),v(0)) = (x_0,v_0)

The goal is to reset position and velocity of the object as fast as possible, meaning:

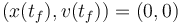(x(t_f),v(t_f)) = (0,0),

with the objective function:

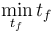
\min\limits_{t_f} t_f

Optimal Control Problem Formulation

The above results in the following OCP

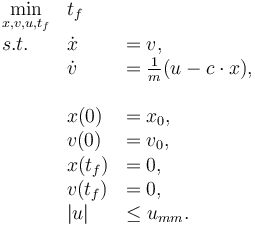
\begin{array}{llll} \min\limits_{x,v,u,t_f} & t_f & & \\ s.t. & \dot x & = v,\\ & \dot v & = \frac{1}{m}(u - c \cdot x),\\ \\ & x(0) & = x_0,\\ & v(0) & = v_0,\\ & x(t_f) & = 0,\\ & v(t_f) & = 0,\\ & |u| & \le u_{mm}.\\ \end{array}

Parameters and Reference Solution

The following parameters were used, to create the reference solution below, with an almost optimal final time 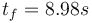t_f = 8.98 s:

m=5, c=10, x_0=2, v_0=5, u_{mm}=5.

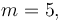
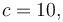
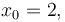
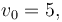
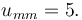
Reference Solution

  • Reference solution plots

  • States and Controls

The OCP was solved within MATLAB R2015b, using the TOMLAB Optimization Package. PROPT reformulates such problems with the direct collocation approach (n=80 collocation points) and automatically finds a suiting solver included in the TOMLAB Optimization Package (in this case, SNOPT was used).

Source Code

References

Retrieved from "https://mintoc.de/index.php?title=Cushioned_Oscillation&oldid=2049"