Difference between revisions of "Car testdrive (elliptic track)"
JonasSchulze (Talk | contribs) m (Text replacement - "<bibreferences/>" to "<biblist />") |
FelixMueller (Talk | contribs) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
|nu = 3 | |nu = 3 | ||
|nw = 1 | |nw = 1 | ||
| + | |nc = 1 | ||
|nri = 7 | |nri = 7 | ||
}} | }} | ||
| − | The elliptic track testdrive problem is a time optimal periodic control problem with gear shift, first introduced in < | + | The elliptic track testdrive problem is a time optimal periodic control problem with gear shift, first introduced in <bib id="Sager2009a" />. |
== Mathematical formulation == | == Mathematical formulation == | ||
| Line 24: | Line 25: | ||
\begin{array}{llcl} | \begin{array}{llcl} | ||
\displaystyle \min_{x(\cdot), u(\cdot), \mu(\cdot)} & t_\text{f} \\[1.5ex] | \displaystyle \min_{x(\cdot), u(\cdot), \mu(\cdot)} & t_\text{f} \\[1.5ex] | ||
| − | \mbox{s.t.} & \dot{x} | + | \mbox{s.t.} & \dot{x} & = & f(t, x, u, \mu), \\ |
& c_\text{x}(t_0) &=& c_\text{x}(t_f), \\ | & c_\text{x}(t_0) &=& c_\text{x}(t_f), \\ | ||
& c_\text{y}(t_0) &=& c_\text{y}(t_f), \\ | & c_\text{y}(t_0) &=& c_\text{y}(t_f), \\ | ||
| Line 31: | Line 32: | ||
& \psi(t_0) &=& \psi(t_f), \\ | & \psi(t_0) &=& \psi(t_f), \\ | ||
& \delta(t_0) &=& \delta(t_f), \\ | & \delta(t_0) &=& \delta(t_f), \\ | ||
| − | & r(t,x | + | & r(t,x,u) &\geq& 0, \\ |
& \mu(t) &\in& \{1, 2, 3, 4, 5\}. | & \mu(t) &\in& \{1, 2, 3, 4, 5\}. | ||
\end{array} | \end{array} | ||
Latest revision as of 09:25, 27 July 2016
| Car testdrive (elliptic track) | |
|---|---|
| State dimension: | 1 |
| Differential states: | 7 |
| Continuous control functions: | 3 |
| Discrete control functions: | 1 |
| Path constraints: | 1 |
| Interior point inequalities: | 7 |
The elliptic track testdrive problem is a time optimal periodic control problem with gear shift, first introduced in [Sager2009a]The entry doesn't exist yet..
Mathematical formulation
The mathematical equations form a small-scale ODE model as presented for the lane change manoeuvre.
The vehicle dynamics are based on a single-track model, derived under the simplifying assumption that rolling and pitching of the car body can be neglected. Consequentially, only a single front and rear wheel is modeled, located in the virtual center of the original two wheels. Motion of the car body is considered on the horizontal plane only.
Four controls represent the driver's choice on steering and velocity. We denote with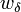 
the steering wheel's angular velocity. The force 
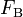controls the total braking force, while the accelerator pedal position 
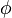is translated into an accelerating force. Finally, the selected gear 
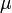influences the effective engine torque's transmission.
Resulting MIOCP
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png)
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x(\cdot), u(\cdot), \mu(\cdot)} & t_\text{f} \\[1.5ex]
\mbox{s.t.} & \dot{x} & = & f(t, x, u, \mu), \\
& c_\text{x}(t_0) &=& c_\text{x}(t_f), \\
& c_\text{y}(t_0) &=& c_\text{y}(t_f), \\
& v(t_0) &=& v(t_f), \\
& \beta(t_0) &=& \beta(t_f) - 2\pi, \\
& \psi(t_0) &=& \psi(t_f), \\
& \delta(t_0) &=& \delta(t_f), \\
& r(t,x,u) &\geq& 0, \\
& \mu(t) &\in& \{1, 2, 3, 4, 5\}.
\end{array}](https://mintoc.de/images/math/f/9/f/f9fe3319664068fb4b4d6cda298428b5.png)
Variants
See testdrive overview page.
References
There were no citations found in the article.
