Difference between revisions of "Lotka Experimental Design"

From mintOC
Jump to: navigation, search
m (correct matrix F)
 
(3 intermediate revisions by 2 users not shown)
Line 3: Line 3:
 
|nx        = 11
 
|nx        = 11
 
|nw        = 2
 
|nw        = 2
 +
|nc        = 4
 
|nre      = 11
 
|nre      = 11
 
}}
 
}}
Line 80: Line 81:
  
 
* [[:Category:AMPL | AMPL]] at [[Lotka Experimental Design (AMPL)]]
 
* [[:Category:AMPL | AMPL]] at [[Lotka Experimental Design (AMPL)]]
 +
* [[:Category: VPLAN | VPLAN code]] at [[Lotka Experimental Design (VPLAN)]]
  
 
== Variants ==
 
== Variants ==
Line 85: Line 87:
 
There are several alternative formulations and variants of the above problem, in particular
 
There are several alternative formulations and variants of the above problem, in particular
  
−
* a prescribed time grid for the control function <bibref>Sager2006</bibref>, see also [[Lotka Experimental Design (AMPL)]],
+
* a prescribed time grid for the control function <bib id="Sager2006" />, see also [[Lotka Experimental Design (AMPL)]],
 
* no fishing, i.e., <math>u \equiv 0</math>,
 
* no fishing, i.e., <math>u \equiv 0</math>,
 
* different fishing control functions for the two species,
 
* different fishing control functions for the two species,
Line 91: Line 93:
  
 
== Miscellaneous and Further Reading ==
 
== Miscellaneous and Further Reading ==
−
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bibref>Sager2006</bibref> and revisited in his PhD thesis <bibref>Sager2005</bibref>. These are also the references to look for more details. The experimental design problem has been described in the habilitation thesis of Sager, <bibref>Sager2011d</bibref>.
+
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bib id="Sager2006" /> and revisited in his PhD thesis <bib id="Sager2005" />. These are also the references to look for more details. The experimental design problem has been described in the habilitation thesis of Sager, <bib id="Sager2011d" />.
  
 
== References ==
 
== References ==
−
<bibreferences/>
+
<biblist />
  
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->

Latest revision as of 09:31, 27 July 2016

Lotka Experimental Design
State dimension: 1
Differential states: 11
Discrete control functions: 2
Path constraints: 4
Interior point equalities: 11


The Lotka Experimental Design problem looks for an optimal fishing strategy to be performed on a fixed time horizon to control the biomasses of both predator as prey fish as described in Lotka Volterra fishing problem. The goal here, however, is to minimize the uncertainty of a follow-up parameter estimation problem. In addition to the fishing decision the question when measurements of the two state variables are performed becomes a degree of freedom.

The mathematical equations form a small-scale ODE model. The ODE from Lotka Volterra fishing problem is extended such that it also includes state sensitivities, the Fisher information matrix entries and integrated sampling states.

The optimal integer control functions shows bang bang behavior.

Mathematical formulation

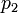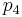We are interested in estimating the parameters p_2 and p_4 of the Lotka-Volterra type predator-prey fish initial value problem

\begin{array}{rcl} \dot{x_1}(t) &=& p_1 \; x_1(t) - p_2 x_1(t) x_2(t) - p_5 u(t) x_1(t), \; t \in [0,t_f], \quad x_1(0) = 0.5, \\ \dot{x_2}(t) &=& - p_3 \; x_2(t) + p_4 x_1(t) x_2(t) - p_6 u(t) x_2(t), \; t \in [0,t_f], \quad x_2(0) = 0.7, \end{array}

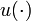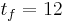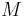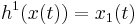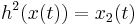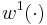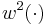where u(\cdot) is a fishing control that may or may not be fixed. The other parameters, the initial values and t_f = 12 are fixed. We are interested in how to fish and when to measure, with an upper bound M on the measuring time. We can measure the states directly, h^1(x(t)) = x_1(t) and h^2(x(t)) = x_2(t). We use two different sampling functions, w^1(\cdot) and w^2(\cdot) in the same experimental setting. This can be seen either as a two-dimensional measurement function 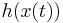h(x(t)), or as a special case of a multiple experiment, in which 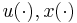u(\cdot), x(\cdot), and G(\cdot) are identical. The experimental design problem then reads

\begin{array}{lll} \displaystyle \min_{x,G,F,z^1,z^2,u,w^1,w^2} && \text{trace} \; \left( F^{-1}(t_f) \right) \\ \text{subject to} \\ \quad \dot{x_1}(t) & = & p_1 \; x_1(t) - p_2 x_1(t) x_2(t) - p_5 u(t) x_1(t),\\ \quad \dot{x_2}(t) & = & - p_3 \; x_2(t) + p_4 x_1(t) x_2(t) - p_6 u(t) x_2(t),\\ \quad \dot{G_{11}}(t) & = & f_{x11}(\cdot) \; G_{11}(t) + f_{x12}(\cdot) \; G_{21}(t) + f_{p12}(\cdot), \\ \quad \dot{G_{12}}(t) & = & f_{x11}(\cdot) \; G_{12}(t) + f_{x12}(\cdot) \; G_{22}(t), \\ \quad \dot{G_{21}}(t) & = & f_{x21}(\cdot) \; G_{11}(t) + f_{x22}(\cdot) \; G_{21}(t), \\ \quad \dot{G_{22}}(t) & = & f_{x21}(\cdot) \; G_{12}(t) + f_{x22}(\cdot) \; G_{22}(t) + f_{p24}(\cdot), \\ \quad \dot{F_{11}}(t) & = & w^1(t) G_{11}(t)^2 + w^2(t) G_{21}(t)^2, \\ \quad \dot{F_{12}}(t) & = & w^1(t) G_{11}(t) G_{12}(t) + w^2(t) G_{21}(t) G_{22}(t), \\ \quad \dot{F_{22}}(t) & = & w^1(t) G_{12}(t)^2 + w^2(t) G_{22}(t)^2, \\ \quad \dot{z^1}(t) & = & w^1(t), \\ \quad \dot{z^2}(t) & = & w^2(t), \\[1.5ex] \quad x(0) &=& (0.5, 0.7), \\ \quad G(0) &=& F(0) = 0, \\ \quad z^1(0) &=& z^2(0) = 0, \\ [1.5ex] \quad u(t) & \in & \mathcal{U}, \; w^1(t) \in \mathcal{W}, \; w^2(t) \in \mathcal{W}, \\ \quad 0 & \le & M - z(t_f) \end{array}

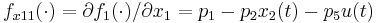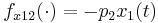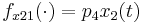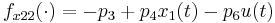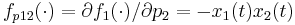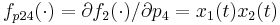with f_{x11}(\cdot) = \partial f_1(\cdot) / \partial x_1 = p_1 - p_2 x_2(t) - p_5 u(t), f_{x12}(\cdot) = - p_2 x_1(t), f_{x21}(\cdot) = p_4 x_2(t), f_{x22}(\cdot) = -p_3 + p_4 x_1(t) - p_6 u(t), and f_{p12}(\cdot) = \partial f_1(\cdot) / \partial p_2 = -x_1(t) x_2(t), f_{p24}(\cdot) = \partial f_2(\cdot) / \partial p_4 = x_1(t) x_2(t).

Note that the state F_{21}(\cdot) = F_{12}(\cdot) has been left out for reasons of symmetry.

Parameters

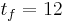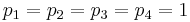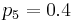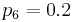We use t_f=12, p_1 = p_2 = p_3 = p_4 = 1, and p_5 = 0.4, p_6 = 0.2. The upper bound on the measurement time intervals is chosen as M=4.

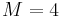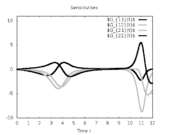
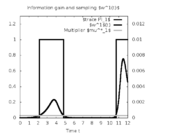
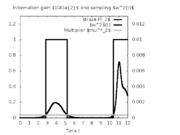
Reference Solutions

Here is one local solution to the above control problem.

  • Reference solution plots

  • States and fishing control.

  • Sensitivities G().

  • Sampling function for first state.

  • Sampling function for second state.

Source Code

Model descriptions are available in

Variants

There are several alternative formulations and variants of the above problem, in particular

  • a prescribed time grid for the control function [Sager2006]Address: Heidelberg
    Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
    Booktitle: Recent Advances in Optimization
    Editor: A. Seeger
    Note: ISBN 978-3-5402-8257-0
    Pages: 269--289
    Publisher: Springer
    Series: Lectures Notes in Economics and Mathematical Systems
    Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
    Volume: 563
    Year: 2009
    Link to Google Scholar    , see also Lotka Experimental Design (AMPL),
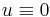  • no fishing, i.e., u \equiv 0,
  • different fishing control functions for the two species,
  • different parameters and start values.

Miscellaneous and Further Reading

The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper [Sager2006]Address: Heidelberg
Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
Booktitle: Recent Advances in Optimization
Editor: A. Seeger
Note: ISBN 978-3-5402-8257-0
Pages: 269--289
Publisher: Springer
Series: Lectures Notes in Economics and Mathematical Systems
Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
Volume: 563
Year: 2009
Link to Google Scholar and revisited in his PhD thesis [Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005
Link to Google Scholar. These are also the references to look for more details. The experimental design problem has been described in the habilitation thesis of Sager, [Sager2011d]Author: S. Sager
How published: University of Heidelberg
Month: August
Note: Habilitation
Title: On the Integration of Optimization Approaches for Mixed-Integer Nonlinear Optimal Control
Url: http://mathopt.de/PUBLICATIONS/Sager2011d.pdf
Year: 2011
Link to Google Scholar.

References

There were no citations found in the article.

Retrieved from "https://mintoc.de/index.php?title=Lotka_Experimental_Design&oldid=2113"