Difference between revisions of "Lotka Volterra fishing problem (AMPL)"

From mintOC
Jump to: navigation, search
m
m (Knitro solution for this benchmark tested by Henry Kar Ming Chan)
Line 95: Line 95:
 
The solution calculated by Bonmin (subversion revision number 1453, default settings, 3 GHz, Linux 2.6.28-13-generic, with ASL(20081205)) has an objective function value of <MATH>\Phi= 1.34434</MATH>, while the optimum of the relaxation is <MATH>\Phi=1.3423368</MATH>. Bonmin needs 35301 iterations and 2741 nodes (4899.97 seconds). Strong branching is done 81 times (1859 iterations), with 0 fathomed nodes and 0 fixed variables. The intervals on the equidistant grid on which <MATH>w(t) = 1</MATH> holds, counting from 0 to 99, are 20-32, 34, 36, 38, 40, 44, 53.
 
The solution calculated by Bonmin (subversion revision number 1453, default settings, 3 GHz, Linux 2.6.28-13-generic, with ASL(20081205)) has an objective function value of <MATH>\Phi= 1.34434</MATH>, while the optimum of the relaxation is <MATH>\Phi=1.3423368</MATH>. Bonmin needs 35301 iterations and 2741 nodes (4899.97 seconds). Strong branching is done 81 times (1859 iterations), with 0 fathomed nodes and 0 fixed variables. The intervals on the equidistant grid on which <MATH>w(t) = 1</MATH> holds, counting from 0 to 99, are 20-32, 34, 36, 38, 40, 44, 53.
  
 +
A faster solution obtained by Knitro version 6.0 under NEOS server environment and tested by Henry Kar Ming Chan. The standard defaults are used except the strong branching strategies and the integrality gap tolerances without parallel features. Final objective value is 1.34521362. Number of nodes processed is 508 and number of subproblems solved is 671. Total program CPU time is 2823.85 seconds with time spent in evaluations for 684.37 seconds. The intervals on the equidistant grid on which <MATH>w(t) = 1</MATH> holds, counting from 0 to 99, are 20-32, 34, 36-37, 42, 44, 52.
 +
 
[[Category:AMPL]]
 
[[Category:AMPL]]

Revision as of 05:14, 17 July 2009

This page contains a discretized version of the MIOCP Lotka Volterra fishing problem in AMPL format. You should be aware of the comments regarding discretization made on the AMPL overview page. Note that you will need to include two generic support AMPL files, ampl_general.mod and ampl_general.dat.

AMPL

The model in AMPL code for a fixed control discretization grid with a collocation method. We need a model file lotka_ampl.mod, 

# ----------------------------------------------------------------
# Lotka Volterra fishing problem with collocation (implicit Euler)
# (c) Sebastian Sager
# ----------------------------------------------------------------
var x {I, 1..nx} >= 0;
param c1 > 0; 
param c2 > 0; 
param ref1 > 0; 
param ref2 > 0;
 
minimize Deviation:
 0.5 * (dt[0]/ntperu) * ( (x[0,1]-ref1)^2 + (x[0,2]-ref2)^2 )
 + 0.5 * (dt[nu-1]/ntperu) * ((x[nt,1]-ref1)^2 + (x[nt,2]-ref2)^2)
 + sum {i in I diff {0,nt} } ( (dt[uidx[i]]/ntperu) * 
   ( (x[i,1] - ref1)^2 + (x[i,2] - ref2)^2 ) ) ;
 
subj to ODE_DISC_1 {i in I diff {0}}:
 x[i,1] = x[i-1,1] + (dt[uidx[i]]/ntperu) * 
  ( x[i,1] - x[i,1]*x[i,2] - x[i,1]*c1*w[uidx[i]] );
 
subj to ODE_DISC_2 {i in I diff {0}}:
 x[i,2] = x[i-1,2] + (dt[uidx[i]]/ntperu) * 
  ( - x[i,2] + x[i,1]*x[i,2] - x[i,2]*c2*w[uidx[i]] );
 
subj to overall_stage_length:
 sum {i in U} dt[i] = T;

a data file lotka_ampl.dat, 

# ------------------------------------
# Data: Lotka Volterra fishing problem
# ------------------------------------
 
# Algorithmic parameters
param ntperu := 100;
param nu := 100;
param nt := 10000;
param nx := 2;
param fix_w := 0;
param fix_dt := 1;
 
# Problem parameters
param T := 12.0;
param c1 := 0.4;   
param c2 := 0.2;
param ref1 := 1.0; 
param ref2 := 1.0;
 
# Initial values differential states
let x[0,1] := 0.5; let x[0,2] := 0.7;
fix x[0,1]; fix x[0,2];
 
# Initial values control
let {i in U} w[i] := 0.0;
for {i in 0..(nu-1) / 2} { let w[i*2] := 1.0; }
let {i in U} dt[i] := T / nu;

and a running script lotka_ampl.run, 

# ------------------------------------
# Solve Lotka Volterra fishing problem
# ------------------------------------
 
model ampl_general.mod;
model ampl_lotka.mod;
data ampl_lotka.dat;
data ampl_general.dat;
 
option presolve_eps 1e-10;
option solver ...;
 
solve;
 
param myt;
let myt := 0;
for {i in I} { 
	if ( dt[uidx[i]] > 1e-6 ) then {
		print myt, w[uidx[i]], x[i,1], x[i,2] > resultInt.txt;
	}
	let myt := myt + (dt[uidx[i]]/ntperu);
}
 
display w;

Results

The solution calculated by Bonmin (subversion revision number 1453, default settings, 3 GHz, Linux 2.6.28-13-generic, with ASL(20081205)) has an objective function value of 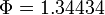\Phi= 1.34434, while the optimum of the relaxation is 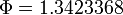\Phi=1.3423368. Bonmin needs 35301 iterations and 2741 nodes (4899.97 seconds). Strong branching is done 81 times (1859 iterations), with 0 fathomed nodes and 0 fixed variables. The intervals on the equidistant grid on which 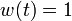w(t) = 1 holds, counting from 0 to 99, are 20-32, 34, 36, 38, 40, 44, 53.

A faster solution obtained by Knitro version 6.0 under NEOS server environment and tested by Henry Kar Ming Chan. The standard defaults are used except the strong branching strategies and the integrality gap tolerances without parallel features. Final objective value is 1.34521362. Number of nodes processed is 508 and number of subproblems solved is 671. Total program CPU time is 2823.85 seconds with time spent in evaluations for 684.37 seconds. The intervals on the equidistant grid on which 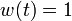w(t) = 1 holds, counting from 0 to 99, are 20-32, 34, 36-37, 42, 44, 52.

Retrieved from "https://mintoc.de/index.php?title=Lotka_Volterra_fishing_problem_(AMPL)&oldid=464"