Difference between revisions of "Van der Pol Oscillator"
ClemensZeile (Talk | contribs) |
|||
| (25 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Dimensions | ||
| + | |nd = 1 | ||
| + | |nx = 2 | ||
| + | |nu = 1 | ||
| + | |nc = 1 | ||
| + | |nre = 2 | ||
| + | }} | ||
| + | |||
The Van der Pol Oscillator is an oscillating system with non-linear damping and self regulation. The System was first introduced by the Dutch physician Balthasar Van der Pol in 1927. The aim is to control the oscillation such that the system stays in a mean position. | The Van der Pol Oscillator is an oscillating system with non-linear damping and self regulation. The System was first introduced by the Dutch physician Balthasar Van der Pol in 1927. The aim is to control the oscillation such that the system stays in a mean position. | ||
| Line 19: | Line 27: | ||
| − | The | + | The Optimal Control Problem arises by adding the objective function: |
<math>\min\limits_{u}\int\limits_{t_0}^{t_f}(x(t)^2+y(t)^2+u(t)^2) dt</math> | <math>\min\limits_{u}\int\limits_{t_0}^{t_f}(x(t)^2+y(t)^2+u(t)^2) dt</math> | ||
| Line 28: | Line 36: | ||
The Optimal Control Problem with the aim to minimize the deflection can be formulated as follows: | The Optimal Control Problem with the aim to minimize the deflection can be formulated as follows: | ||
| − | <math> \begin{array}{ | + | <math> |
| − | + | \begin{array}{lll} | |
| − | + | \min\limits_{u} & \int\limits_{t_0}^{t_f} & (x(t)^2+y(t)^2+u(t)^2) dt\\ | |
| − | + | s.t. & \dot x & = y,\\ | |
| − | & x(0)=1\\ | + | & \dot y & = u(1-x^2) y-x,\\ |
| − | & y(0)=0\\ | + | & x(0) & =1,\\ |
| − | & u\le 0.75\\ | + | & y(0) & =0,\\ |
| − | + | & u(t) & \le 0.75.\\ | |
| − | + | \end{array}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
== Parameters == | == Parameters == | ||
| Line 50: | Line 55: | ||
== Reference Solution == | == Reference Solution == | ||
| − | The following reference solution was generated using JModelica with the automatic differentiation tool CasADI and the solver IPOPT. The Optimica code used to solve the problem can be found under | + | The following reference solution was generated using JModelica with the automatic differentiation tool CasADI and the solver IPOPT. The Optimica code used to solve the problem can be found under [[Van der Pol Oscillator (JModelica)]] The optimal value of the objective function is 3.1762. |
| − | + | ||
| + | |||
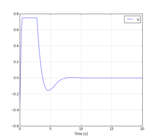
| + | <gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2"> | ||
| + | Image:VDP_Plot_control.png| Control u over time (damping). | ||
| + | Image:VDP_Plot_states.png| Position coordinate x and it's derivative y. | ||
| + | Image:VDP_Plot_derivatives.png| Derivative <math>\dot x</math> and second derivative <math>\dot y</math>. | ||
| + | </gallery> | ||
== Source Code == | == Source Code == | ||
Model descriptions are available in: | Model descriptions are available in: | ||
| − | + | ||
| − | + | * [[:Category: JModelica | JModelica code]] at [[Van der Pol Oscillator (JModelica)]] | |
| − | + | * [[:Category: Julia/JuMP | JuMP code]] (of a slightly modified Van der Pol oscillator problem) at [[Van der Pol Oscillator (Jump)]] | |
| + | |||
| + | == Variants == | ||
| + | |||
| + | There are several alternative formulations and variants of the above problem, in particular | ||
| + | |||
| + | * a variant where partial outer convexification is applied on the control and the continous control is replaces by binary controls, see also [[Van der Pol Oscillator (binary variant)]], | ||
| + | |||
| + | |||
| + | == References == | ||
| + | The Problem can be found under the following [https://en.wikipedia.org/wiki/Van_der_Pol_oscillator link] or in the [http://www.jmodelica.org/api-docs/usersguide/1.4.0/ch08s02.html JModelica Users Guide]. | ||
| + | |||
| + | [[Category:MIOCP]] | ||
| + | [[Category:Bang bang]] | ||
| + | [[Category:Path-constrained arcs]] | ||
| + | [[Category:ODE model]] | ||
Latest revision as of 18:27, 10 January 2018
| Van der Pol Oscillator | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Continuous control functions: | 1 |
| Path constraints: | 1 |
| Interior point equalities: | 2 |
The Van der Pol Oscillator is an oscillating system with non-linear damping and self regulation. The System was first introduced by the Dutch physician Balthasar Van der Pol in 1927. The aim is to control the oscillation such that the system stays in a mean position.
Contents
[hide]Model formulation
The Van der Pol Oscillator evolves over time according to the second order differential equation:
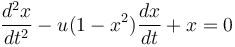
where 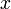 is the position coordinate, which is a function of the time
is the position coordinate, which is a function of the time 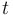 , and
, and 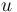 is a scalar parameter indicating the non-linearity and the strength of the damping.
is a scalar parameter indicating the non-linearity and the strength of the damping.
For 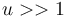 the oscillator is being damped, whereas for
the oscillator is being damped, whereas for 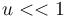 energy is added to the system.
energy is added to the system.
Based on the transformation 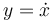 the problem can be reformulated:
the problem can be reformulated:
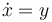
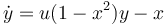
The Optimal Control Problem arises by adding the objective function:
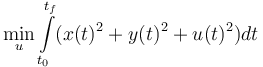
Optimal Control Problem
The Optimal Control Problem with the aim to minimize the deflection can be formulated as follows:
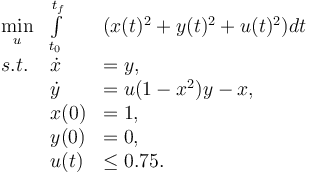
Parameters
These fixed values are used within the model:
![[t_0,t_f]=[0,20]](https://mintoc.de/images/math/d/4/a/d4a8409487693407b169d542957e0321.png)
Reference Solution
The following reference solution was generated using JModelica with the automatic differentiation tool CasADI and the solver IPOPT. The Optimica code used to solve the problem can be found under Van der Pol Oscillator (JModelica) The optimal value of the objective function is 3.1762.
- Reference solution plots
Source Code
Model descriptions are available in:
- JModelica code at Van der Pol Oscillator (JModelica)
- JuMP code (of a slightly modified Van der Pol oscillator problem) at Van der Pol Oscillator (Jump)
Variants
There are several alternative formulations and variants of the above problem, in particular
- a variant where partial outer convexification is applied on the control and the continous control is replaces by binary controls, see also Van der Pol Oscillator (binary variant),
References
The Problem can be found under the following link or in the JModelica Users Guide.


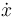 and second derivative
and second derivative 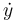 .
.