Difference between revisions of "D'Onofrio chemotherapy model"

From mintOC
Jump to: navigation, search
(→‎Mathematical formulation)
 
(7 intermediate revisions by one other user not shown)
Line 3: Line 3:
 
|nx        = 4
 
|nx        = 4
 
|nu        = 2
 
|nu        = 2
 +
|nc        = 4
 
}}
 
}}
  
Line 19: Line 20:
 
             & \dot{x}_2 & = & u_0,  \\
 
             & \dot{x}_2 & = & u_0,  \\
 
             & \dot{x}_3 & = & u_1, \\ [1.5ex]
 
             & \dot{x}_3 & = & u_1, \\ [1.5ex]
−
             & 0 & \leq & u_0 \leq  u_0^{max}, \\
+
             & u_0 & \in & [0,u_0^{max}],\\
−
             & 0 & \leq & u_1 \leq u_1^{max}, \\
+
             & u_1 & \in & [0,u_1^{max}],\\
 
             & x_2 & \leq & x_2^{max},  \\
 
             & x_2 & \leq & x_2^{max},  \\
 
             & x_3 & \leq & x_3^{max}.
 
             & x_3 & \leq & x_3^{max}.
Line 91: Line 92:
 
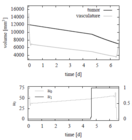
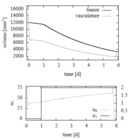
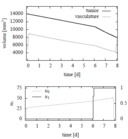
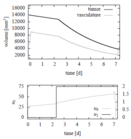
  Image:d'Onofrio 4.png| Optimal controls and states with parameter set 4.
 
  Image:d'Onofrio 4.png| Optimal controls and states with parameter set 4.
 
</gallery>
 
</gallery>
 +
 +
== Variants ==
 +
 +
* a variant where partial outer convexification is applied on the control and the continous control is replaces by binary controls, see also [[D'Onofrio model (binary variant)]],
 +
  
 
==Source Code==
 
==Source Code==
  
−
[[:Category:Muscod | Muscod code]]  
+
* [[:Category:Muscod | Muscod code]] at [[D'Onofrio chemotherapy model (Muscod)]]
−
<source lang="cpp">
+
−
/* volume of tumor */
+
−
rhs[0] = - zeta*x[0]*log(x[0]/x[1])-F*x[0]*u1_;
+
−
/* volume of neighboring blood vessels */
+
−
rhs[1] = b*x[0] - (mu + d*pow(x[0],2.0/3.0))*x[1] - G*u0_*x[1] - eta*x[1]*u1_;
+
−
/* amount of anti-angiogetic drug */
+
−
rhs[2] = u0_;
+
−
/* amount of cytostatic drug */
+
−
rhs[3] = u1_;
+
−
</source>
+
  
 
== References ==
 
== References ==
 
<biblist />
 
<biblist />
  
−
[[Category:Medicine]]
 
 
[[Category:MIOCP]]
 
[[Category:MIOCP]]
 +
[[Category:Medicine]]
 
[[Category:ODE model]]
 
[[Category:ODE model]]
 +
[[Category:Bang bang]]
 +
[[Category:Path-constrained arcs]]

Latest revision as of 14:31, 11 January 2018

D'Onofrio chemotherapy model
State dimension: 1
Differential states: 4
Continuous control functions: 2
Path constraints: 4


This cancer chemotherapy model is based on the work of d'Onofrio. The corresponding dynamic describes the effect of two different drugs administered to the patient. An anti-angiogetic drug is used to suppress the formation of blood vessels from existing vessels and thereby starving the tumors supply of proliferating vessels. In addition a cytostatic drug effects the proliferation of the tumor cells directly. The dynamic of the problem is given by an ODE model.

Mathematical formulation

For t \in [t_0, t_f] the optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, u} & x_0(t_f) &+& \alpha \int_{t_0}^{t_f} u_0(t)^2 \text{d}t \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & - \zeta x_0 \text{ln} \left( \frac{x_0}{x_1} \right) - F \; x_0 u_1, \\ & \dot{x}_1 & = & b x_0 - \mu x_1 - d x_0^{\frac{2}{3}}x_1 - G u_0 x_1 - \eta x_1 u_1, \\ & \dot{x}_2 & = & u_0, \\ & \dot{x}_3 & = & u_1, \\ [1.5ex] & u_0 & \in & [0,u_0^{max}],\\ & u_1 & \in & [0,u_1^{max}],\\ & x_2 & \leq & x_2^{max}, \\ & x_3 & \leq & x_3^{max}. \end{array}

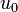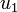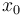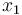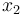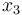where the control u_0 denotes the administered amount of anti-angiogetic drugs and u_1 the amount of cytostatic drugs. The state x_0 describes the volume of tumor and x_1 the volume of neighboring blood vessels. The remaining states x_2 and x_3 are used to constraint the maximum amount of drugs over the duration of the therapy.

Parameters

In the model these parameters are fixed.

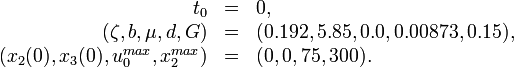
\begin{array}{rcl} t_0 &=& 0,\\ (\zeta, b, \mu, d, G) &=& (0.192, 5.85, 0.0, 0.00873, 0.15),\\ (x_2(0), x_3(0), u_0^{max}, x_2^{max}) &=& (0,0,75,300). \end{array}

The parameters 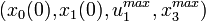(x_0(0), x_1(0), u_1^{max}, x_3^{max}) can be taken from the parameter sets shown in the following section. To the remaining parameters 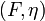(F, \eta) exists no experimental data.

Reference Solutions

The problem can be solved with the [multiple shooting method]. For the following solutions the control functions and states are discretized on the same grid, with 100 nodes. The unknown parameters are chosen from the following parameter sets

Parameter set 1

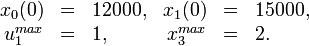
\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}

Parameter set 2

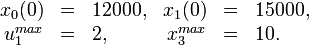
\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}

Parameter set 3

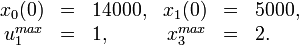
\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}

Parameter set 4

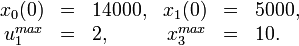
\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}

Furthermore in the objective function 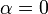\alpha =0 is chosen.

  • Reference solution plots

  • Optimal controls and states computed with a multiple shooting approach on the same discretization grid with 100 nodes and parameter set 1.

  • Optimal controls and states with parameter set 2.

  • Optimal controls and states with parameter set 3.

  • Optimal controls and states with parameter set 4.

Variants

  • a variant where partial outer convexification is applied on the control and the continous control is replaces by binary controls, see also D'Onofrio model (binary variant),


Source Code

References

There were no citations found in the article.

Retrieved from "https://mintoc.de/index.php?title=D%27Onofrio_chemotherapy_model&oldid=2223"