Difference between revisions of "Methanol to Hydrocarbons problem"
From mintOC
FelixMueller (Talk | contribs) |
FelixMueller (Talk | contribs) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
|nz = 3 | |nz = 3 | ||
|np = 5 | |np = 5 | ||
| + | |nc = 5 | ||
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | ||
| Line 17: | Line 18: | ||
\displaystyle \min_{\theta} &\sum\limits_{j=1}^{16} &&||y(\tau_j; \theta) - z_j||^2 \\[1.5ex] | \displaystyle \min_{\theta} &\sum\limits_{j=1}^{16} &&||y(\tau_j; \theta) - z_j||^2 \\[1.5ex] | ||
\mbox{s.t.} | \mbox{s.t.} | ||
| − | & \dot{y}_1 & = & -( 2 \theta_2 - \frac{\theta_1 y_2}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 + \theta_4) y_1, \\ | + | & \dot{y}_1 & = & -( 2 \theta_2 - \frac{\theta_1 y_2}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 + \theta_4) y_1, \\[0.3cm] |
| − | & \dot{y}_2 & = & \frac{\theta_1 y_1 (\theta_2 y_1 - y_2)}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 y_1, \\ | + | & \dot{y}_2 & = & \frac{\theta_1 y_1 (\theta_2 y_1 - y_2)}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 y_1, \\[0.3cm] |
| − | & \dot{y}_3 & = & \frac{\theta_1 y_1 (y_2 + \theta_5 y_1}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_4 y_1, \\ | + | & \dot{y}_3 & = & \frac{\theta_1 y_1 (y_2 + \theta_5 y_1}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_4 y_1, \\[0.3cm] |
| − | & \theta_i & \geq & 0. | + | & \theta_i & \geq & 0 \quad i = 1,...,5. |
\end{array} | \end{array} | ||
</math> | </math> | ||
Latest revision as of 09:32, 27 July 2016
| Methanol to Hydrocarbons problem | |
|---|---|
| Algebraic states: | 3 |
| Continuous control values: | 5 |
| Path constraints: | 5 |
The Methanol to Hydrocarbons problem tries to determine "reaction coefficients for the conversion of methanol into various hydrocarbons." (Cite and problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{\theta} &\sum\limits_{j=1}^{16} &&||y(\tau_j; \theta) - z_j||^2 \\[1.5ex]
\mbox{s.t.}
& \dot{y}_1 & = & -( 2 \theta_2 - \frac{\theta_1 y_2}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 + \theta_4) y_1, \\[0.3cm]
& \dot{y}_2 & = & \frac{\theta_1 y_1 (\theta_2 y_1 - y_2)}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_3 y_1, \\[0.3cm]
& \dot{y}_3 & = & \frac{\theta_1 y_1 (y_2 + \theta_5 y_1}{(\theta_2 + \theta_5) y_1 + y_2} + \theta_4 y_1, \\[0.3cm]
& \theta_i & \geq & 0 \quad i = 1,...,5.
\end{array}](https://mintoc.de/images/math/f/c/4/fc4a9478c894191036370aa1c2d64751.png)
Parameters
The values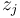 
are measurements for the concentration for 
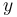at time points 
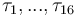and initial conditions are known.
Source Code
Model descriptions are available in
