Difference between revisions of "Category:Solution characterization"
m (New page: In this category all sub-categories are listed that describe specific behavior of an optimal solution. Hence, all problems can be identified that share common characteristics, such as an o...) |
FelixMueller (Talk | contribs) |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle <bib id="Pontryagin1962" /> applied here only to the relaxation of the binary control functions <math>\omega(\cdot)</math>, denoted by <math>\alpha(\cdot) \in [0,1]^{n_\omega}</math>. In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, <bib id="Srinivasan2003" />, where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs. | |
| + | |||
| + | Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs. | ||
| + | |||
| + | == References == | ||
| + | <biblist /> | ||
| + | |||
[[Category:Problem characterization]] | [[Category:Problem characterization]] | ||
Latest revision as of 13:58, 28 January 2016
The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle [Pontryagin1962]Address: Chichester
Author: Pontryagin, L.S.; Boltyanski, V.G.; Gamkrelidze, R.V.; Miscenko, E.F.
Publisher: Wiley
Title: The Mathematical Theory of Optimal Processes
Year: 1962
applied here only to the relaxation of the binary control functions 
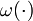, denoted by ![\alpha(\cdot) \in [0,1]^{n_\omega}](https://mintoc.de/images/math/6/d/4/6d44af77747bea2951d669a09e98b55d.png)
. In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, [Srinivasan2003]Author: Srinivasan, B.; Palanki, S.; Bonvin, D.
Journal: Computers \& Chemical Engineering
Pages: 1--26
Title: Dynamic Optimization of Batch Processes: I. Characterization of the Nominal Solution
Volume: 27
Year: 2003, where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs.
Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs.
References
There were no citations found in the article.
Subcategories
This category has the following 5 subcategories, out of 5 total.
