Difference between revisions of "Continuously Stirred Tank Reactor problem"
FelixMueller (Talk | contribs) (Created page with "{{Dimensions |nd = 1 |nx = 4 |nu = 2 |nre = 2 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... -->The Continuously...") |
ClemensZeile (Talk | contribs) (→Parameters) |
||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 9: | Line 9: | ||
The inflow into the tank contains only cyclopentadiene (substance <math> A </math>) with temperature <math> \theta_0 </math> and the flow rate <math> \dot{V} </math> can be controlled. The outflow rate is the same as the inflow rate to keep the liquid level in the tank constant. | The inflow into the tank contains only cyclopentadiene (substance <math> A </math>) with temperature <math> \theta_0 </math> and the flow rate <math> \dot{V} </math> can be controlled. The outflow rate is the same as the inflow rate to keep the liquid level in the tank constant. | ||
| − | "The outflow contains a remainder of cyclopentadiene, the wanted product cyclepentenol (substance <math> B </math>) and two unwated by-products, cyclopentanediol (substance <math> C </math>) and dicyclopentadiene (substance <math> D </math>) with concentrations <math> c_A, c_B, c_C, | + | "The outflow contains a remainder of cyclopentadiene, the wanted product cyclepentenol (substance <math> B </math>) and two unwated by-products, cyclopentanediol (substance <math> C </math>) and dicyclopentadiene (substance <math> D </math>) with concentrations <math> c_A, c_B, c_C, c_D </math>." The latter two are not tracked in the problem as the substances are not of use. |
The reaction scheme is given as: | The reaction scheme is given as: | ||
| Line 66: | Line 66: | ||
|Arrhenius coefficient | |Arrhenius coefficient | ||
|<math>k_{30}</math> | |<math>k_{30}</math> | ||
| − | |<math> 9.043 \cdot 10^{ | + | |<math> 9.043 \cdot 10^{9} </math> |
|<math> h^{-1} </math> | |<math> h^{-1} </math> | ||
|- | |- | ||
| Line 144: | Line 144: | ||
|<math> ^\circ C </math> | |<math> ^\circ C </math> | ||
|} | |} | ||
| − | |||
== Reference solution == | == Reference solution == | ||
Latest revision as of 12:11, 2 September 2019
| Continuously Stirred Tank Reactor problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 4 |
| Continuous control functions: | 2 |
| Interior point equalities: | 2 |
The Continuously Stirred Tank Reactor problem considers a chemical reaction that produces cyclopenthenol while using up cyclepentadiene "by an acid-catalyzed electrophilic hydration in aqueous solution", an exothermal reaction which needs to be cooled. This problem can e.g. be found in [Diehl2001]Author: M. Diehl
School: Universit\"at Heidelberg
Title: Real-Time Optimization for Large Scale Nonlinear Processes
Url: http://www.ub.uni-heidelberg.de/archiv/1659/
Year: 2001 .
.
The inflow into the tank contains only cyclopentadiene (substance 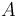 ) with temperature
) with temperature 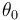 and the flow rate
and the flow rate 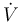 can be controlled. The outflow rate is the same as the inflow rate to keep the liquid level in the tank constant.
"The outflow contains a remainder of cyclopentadiene, the wanted product cyclepentenol (substance
can be controlled. The outflow rate is the same as the inflow rate to keep the liquid level in the tank constant.
"The outflow contains a remainder of cyclopentadiene, the wanted product cyclepentenol (substance 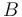 ) and two unwated by-products, cyclopentanediol (substance
) and two unwated by-products, cyclopentanediol (substance 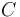 ) and dicyclopentadiene (substance
) and dicyclopentadiene (substance 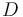 ) with concentrations
) with concentrations 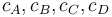 ." The latter two are not tracked in the problem as the substances are not of use.
The reaction scheme is given as:
." The latter two are not tracked in the problem as the substances are not of use.
The reaction scheme is given as:
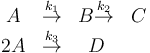
where the reaction rates 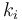 are a function of the reactor temperature
are a function of the reactor temperature 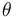 via an Arrhenius law
via an Arrhenius law
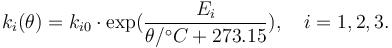
"The temperature 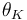 in the cooling jacket is held down by an external heat exchanger whose heat removal rate
in the cooling jacket is held down by an external heat exchanger whose heat removal rate 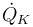 can be controlled."
can be controlled."
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \max_{\dot{V}, \dot{Q}_K} & c_B & & \text{ at the end of reaction} \\[1.5ex]
\mbox{s.t.}
& \dot{c_A} & = & \frac{\dot{V}}{V_R} (c_{A0} - c_A) - k_1 c_A - k_3 c_A^2, \\[0.5cm]
& \dot{c_B} & = & -\frac{\dot{V}}{V_R} c_B + k_1 c_A - k_2 c_B, \\[0.5cm]
& \dot{\theta} & = & \frac{\dot{V}}{V_R} ( \theta_0 - \theta) + \frac{k_w A_R}{\rho C_p V_R} (\theta_K - \theta) - \frac{1}{\rho C_p} (k_1 c_A H_1 + k_2 c_B H_2 + k_3 c_A^2 H_3), \\[0.5cm]
& \dot{\theta_K} & = & \frac{1}{m_K C_{PK}} ( \dot{Q}_K + k_w A_R (\theta - \theta_K)),\\[0.7cm]
& c_A(0) & = & c_{A0},\\
& c_B(0) & = & 0.
\end{array}](https://mintoc.de/images/math/2/0/b/20b7b101b37faf8a30c9ec08ad431f20.png)
where the various values are given in the Parameters section.
Parameters
These fixed values are used within the model.
| Name | Symbol | Value | Unit |
| Arrhenius coefficient | 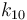
|
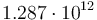
|
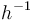
|
| Arrhenius coefficient | 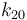
|
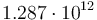
|
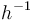
|
| Arrhenius coefficient | 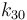
|
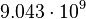
|
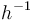
|
| Arrhenius coefficient | 
|
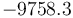
|
[-] |
| Arrhenius coefficient | 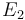
|
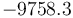
|
[-] |
| Arrhenius coefficient | 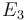
|
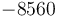
|
[-] |
| Reaction enthalpy | 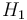
|
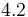
|
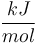
|
| Reaction enthalpy | 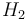
|
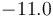
|
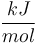
|
| Reaction enthalpy | 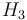
|
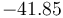
|
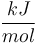
|
| Solution density | 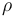
|
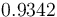
|
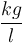
|
| Capacity of aqueous solution | 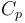
|
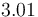
|
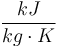
|
| Heat transfer coefficient for cooling jacket | 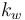
|
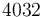
|
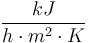
|
| Reactor surface area | 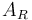
|
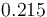
|
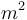
|
| Reactor volume | 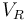
|
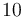
|
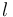
|
| Coolant mass | 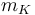
|
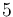
|
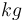
|
| Capacity of coolant solution | 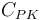
|
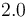
|
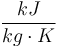
|
Starting concentration of subs. 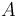
|
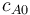
|
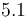
|
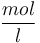
|
| Inflow temperature | 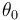
|
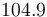
|
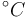
|
Reference solution
"The result of a steady state optimization of the yield 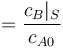 with respect to the design parameter
with respect to the design parameter 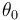 (feed temperature) and the two controls yields the steady stae and controls"
(feed temperature) and the two controls yields the steady stae and controls"
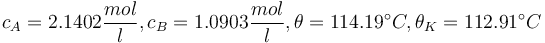 and
and 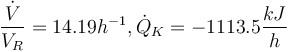 .
.
Source Code
Model descriptions are available in