Difference between revisions of "LinearMetabolic"
m (Tsiantis reference) |
(→Data) |
||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
|nd = 1 | |nd = 1 | ||
|nx = 4 | |nx = 4 | ||
| − | | | + | |nu = 3 |
| − | |nc = | + | |nc = 1 |
| − | |nri | + | |nri = 0 |
|nre = 5 | |nre = 5 | ||
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | ||
--> | --> | ||
| − | + | The '''Linear Metabolic problem''' is a generalized inverse optimal control problem formulated and investigated in <bib id="Tsiantis2018" />. It tries to identify an a priori unknown objective function from data. | |
| − | The | + | The problem is a generalization of the one studied by de Hijas-Liste et al. (2014), where it was considered as a standard optimal control problem (OCP). Here, we take the solution reference of the inner problem as the multi-objective OCP described in de Hijas-Liste et al. (2014), selecting a specific point of the resulting Pareto front. This case study is interesting, because it includes path constraints on the states and the inputs. |
| − | + | A 3-step linear metabolic pathway with mass action kinetics is considered. The differential states <math>x</math> are metabolite concentrations, the time-dependent control functions <math>u</math> are enzyme concentrations, and the model parameters <math>p</math> are kinetic parameters in mass action expressions. Candidate objective functionals <math>\phi</math> are the final time and the time-integral of the intermediate metabolite concentrations. The measurement function is a map to the values of the differential states and comprises measurements of metabolite concentrations. The differential equations are assumed to be fully known as standard mass action kinetics. An inequality path constraint is present (but potentially unknown in such settings) on the inner level and critical from a biological point of view: limitations due to molecular crowding impose an upper bound on the maximum total concentration of enzymes (controls) at any given time. Boundary conditions are fixed initial and terminal values of the metabolite concentrations. | |
== Mathematical formulation == | == Mathematical formulation == | ||
| − | The | + | The gIOC is given by |
| − | + | <math> | |
| − | <math> | + | \displaystyle \min_{(p, w, x^*, u^*, T^*)} \; \| x^* - \eta \| |
| − | + | </math> | |
| − | + | subject to | |
| − | + | <math> | |
| − | + | (x^*,u^*, T^*) \in \displaystyle \arg \min_{x, u, T} w_1 \cdot \int_{0}^{T} (x_2 + x_3) \, dt + w_2 \cdot \int_{0}^{T} 1 \,dt | |
| − | + | </math> | |
| − | + | subject to | |
| − | + | <math> | |
| − | + | \begin{array}{rcl} | |
| − | & | + | \dot{x_1}(t) &=& \displaystyle 0 \\ |
| − | + | \dot{x_2}(t) &=& \displaystyle p_1 \cdot x_1 \cdot u_1 - p_2 \cdot x_2 \cdot u_2 \\ | |
| − | & | + | \dot{x_3}(t) &=& \displaystyle p_2 \cdot x_2 \cdot u_2 - p_3 \cdot x_3 \cdot u_3 \\ |
| − | \end{array} | + | \dot{x_4}(t) &=& \displaystyle p_3 \cdot x_3 \cdot u_3 \\ |
| − | </math> | + | x(0) &=& (1, 0, 0, 0) \\ |
| − | + | x_4(T) &=& 0.9 \\ | |
| − | Here the four differential states stand for the | + | x_i(t) &\ge& 0 \; \forall \; i \in \{1,2,3,4\} \\ |
| + | u_i(t) &\in& [0,1] \; \forall \; i \in \{1,2,3\} \\ | ||
| + | 1 &\ge& u_1(t) + u_2(t) + u_3(t) \\ | ||
| + | w_1, w_2 \in [0,1] \\ | ||
| + | w_1 + w_2 = 1 | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Here the four differential states and three control functions stand for the metabolite concentrations (<math> x_1, x_2, x_3, x_4 </math>) and the enzyme concentrations (<math> u_1, u_2, u_3 </math>). The two objective function candidates are the sum of intermediate metabolite concentrations and the transition time. The three model parameters <math>p_1, p_2, p_3</math> are kinetic parameters in mass action expressions. | ||
| + | |||
| + | == Data == | ||
| + | |||
| + | The following table gives different values for <math>\eta</math>, componentwise for all four entries of <math>x</math> as time series, for different combinations of weights and noise levels that were used to produce the synthetic data via solution of forward optimal control problems. | ||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| − | |+ | + | |+Data |
|- | |- | ||
| − | | | + | |weights <math>w_1, w_2</math> |
| − | | | + | |parameters <math>p_1, p_2, p_3</math> |
| − | | | + | |noise |
| − | | | + | |number of time intervals <math>N</math> |
| + | |final time <math>T^*</math> | ||
| + | |data <math>\eta</math> | ||
|- | |- | ||
| − | | | + | |[0.232, 0.768] |
| − | | | + | |[1,1,1] |
| − | | | + | | 0 |
| − | |[ | + | |20 |
| + | |4.3 | ||
| + | | | ||
| + | [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], | ||
| + | [0, 0.215, 0.4298, 0.6446, 0.8593, 1.074, 1.2885, 1.503, 1.6591, 1.3381, 1.0792, 0.8704, 0.7021, 0.5662, 0.4849, 0.4846, 0.4844, 0.4842, 0.484, 0.4838, 0.4836], | ||
| + | [0, 0.0, 0.0002, 0.0004, 0.0007, 0.001, 0.0015, 0.002, 0.0391, 0.36, 0.6186, 0.827, 0.9948, 1.1301, 1.1405, 0.92, 0.7423, 0.5989, 0.4832, 0.3899, 0.3147], | ||
| + | [0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0001, 0.0004, 0.0008, 0.0013, 0.0019, 0.0729, 0.2935, 0.4715, 0.6152, 0.731, 0.8245, 0.9]] | ||
|- | |- | ||
| − | | | + | |[0.232, 0.768] |
| − | | | + | |[1,1,1] |
| − | | | + | |0.2 |
| − | | | + | |20 |
| + | |4.3 | ||
| + | | | ||
| + | [[1., 0.9590812,0.82266497,0.95877308,0.60614596,1.20781224, 0.92205471,1.0215116 ,0.89080449,1.05747735,1.04019676,1.06665347, 0.78545416,1.17084962,1.08658091,1.01467309,0.91098074,1.10349004, 0.83411596,0.73187308,0.70399766], | ||
| + | [0.,0.37493181,0.10514573,0.79448823,0.44666767,1.19676033,1.14532119,1.64453389,1.93572019,1.37435635,0.92790967,1.11928728, 0.52061388,0.43837628,0.31518386,0.50300858,0.52891948,0.74255261, 0.07589526,0.64051491,0.47184952], | ||
| + | [ 0., 0.23680072, 0.05047157,-0.03770305, 0.34603556,-0.45259701,0.25340369, 0.25177705, 0.16210031, 0.34367395, 0.96197961, 1.10224845, 1.21656021, 1.38442255, 1.02149302, 0.68818982, 0.7921558 , 0.32238544, 0.30229594, 0.43876605, 0.22073986], | ||
| + | [ 0.,-0.01591557,-0.12432336,-0.17669569,-0.21325853,-0.2489822 , -0.22989873,-0.0564741 ,-0.19961696,-0.16036058,-0.04386598, 0.25004781, -0.07279584, 0.09573081,-0.12329308,-0.03451486, 0.0173815 , 0.79895333, 0.8178261 , 0.53498205, 1.1021996]] | ||
|- | |- | ||
| − | | | + | |[0,1] |
| − | | | + | |[1,1,1] |
| − | |0 | + | |0 |
| − | |[-] | + | |20 |
| + | |4.226 | ||
| + | | | ||
| + | [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], | ||
| + | [0, 0.211317, 0.422635, 0.633952, 0.845269, 1.05659, 1.2679, 1.47922, 1.69054, 1.90186, 1.95601, 1.58342, 1.2818, 1.03764, 0.839981, 0.685458, 0.685458, 0.685458, 0.685458, 0.685458, 0.685458], | ||
| + | [0, 3.40252e-10, 2.02262e-09, 6.04129e-09, 1.32631e-08, 2.47434e-08, 4.23248e-08, 6.98021e-08, 1.16723e-07, 2.20847e-07, 0.103509, 0.476095, 0.777716, 1.02188, 1.21954, 1.36367, 1.10391, 0.893635, 0.72341, 0.58561, 0.474061], | ||
| + | [0, 2.79389e-19, 2.05361e-18, 7.26553e-18, 1.82666e-17, 3.77412e-17, 6.87107e-17, 1.14894e-16, 1.82155e-16, 2.86358e-16, 3.73778e-11, 7.31532e-10, 5.75723e-09, 2.28945e-08, 7.3467e-08, 0.0103927, 0.270148, 0.480425, 0.65065, 0.78845, 0.9]] | ||
|- | |- | ||
| − | | | + | |[0,1] |
| − | | | + | |[1,1,1] |
| − | + | |0.1 | |
| − | + | |20 | |
| − | + | |4.226 | |
| − | + | | | |
| − | + | [[1.,0.98392517,1.02825092,1.0127091 ,1.21814838,1.03987996, 1.17367563,1.0721497 ,1.11254303,0.91560159,0.92664064,0.93069442, 1.01285111,1.10017347,0.9952073 ,1.05616016,1.12564585,1.02743444, 0.93306189,1.04808763,0.87659083], | |
| − | |0. | + | [0.,0.19112834,0.6016258 ,0.70894548,0.86077117,0.95316772, 1.12244906,1.51535841,1.48548905,1.87282215,2.13181979,1.48523121, 1.14624017,1.06839771,0.8838448 ,0.72466348,0.61379013,0.70096009, 0.73549769,0.62452413,0.61907767], |
| − | | | + | [0., 0.04514029,-0.06510522,-0.00304812,-0.01620013, 0.006101, 0.04992798, 0.29317191, 0.11305888, 0.2285637 , 0.26142926, 0.50457228, 0.87829835, 0.90900075, 1.32279588, 1.42225272, 1.18086941, 0.67720058, 0.61562944, 0.6339817 , 0.36613472], |
| − | | | + | [0.,-0.13882966, 0.18200648,-0.06629627,-0.01496019, 0.21349797,-0.10124824,-0.05505019, 0.23235014, 0.09448396, 0.06059911,-0.12137716, -0.00781841, 0.04355511, 0.1369212 ,-0.13011339, 0.2027646 , 0.51512985, 0.65331917, 0.78324169, 0.81304223]] |
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
|} | |} | ||
| − | == | + | == Examples == |
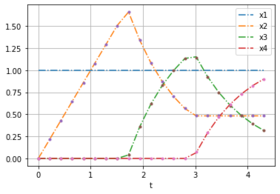
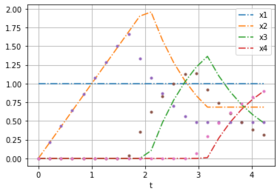
| − | + | The plots show noise free data for different weights from forward optimal control problems. | |
| − | + | <gallery caption="Solution plots" widths="280px" heights="240px" perrow="3"> | |
| − | + | Image:LPN3B_min_sum_data.png| OCP with weights [0.232, 0.768]. | |
| − | + | Image:LPN3B_minT_x_data.png| OCP with weights [0,1]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <gallery caption=" | + | |
| − | Image: | + | |
| − | + | ||
| − | Image: | + | |
</gallery> | </gallery> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Latest revision as of 06:17, 23 October 2023
| LinearMetabolic | |
|---|---|
| State dimension: | 1 |
| Differential states: | 4 |
| Continuous control functions: | 3 |
| Path constraints: | 1 |
| Interior point inequalities: | 0 |
| Interior point equalities: | 5 |
The Linear Metabolic problem is a generalized inverse optimal control problem formulated and investigated in [Tsiantis2018]Author: Tsiantis, Nikolaos; Balsa-Canto, Eva; Banga, Julio R
Journal: Bioinformatics
Number: 14
Pages: 2433-2440
Title: Optimality and identification of dynamic models in systems biology: an inverse optimal control framework
Volume: 34
Year: 2018 . It tries to identify an a priori unknown objective function from data.
. It tries to identify an a priori unknown objective function from data.
The problem is a generalization of the one studied by de Hijas-Liste et al. (2014), where it was considered as a standard optimal control problem (OCP). Here, we take the solution reference of the inner problem as the multi-objective OCP described in de Hijas-Liste et al. (2014), selecting a specific point of the resulting Pareto front. This case study is interesting, because it includes path constraints on the states and the inputs.
A 3-step linear metabolic pathway with mass action kinetics is considered. The differential states 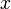 are metabolite concentrations, the time-dependent control functions
are metabolite concentrations, the time-dependent control functions 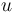 are enzyme concentrations, and the model parameters
are enzyme concentrations, and the model parameters 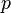 are kinetic parameters in mass action expressions. Candidate objective functionals
are kinetic parameters in mass action expressions. Candidate objective functionals 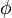 are the final time and the time-integral of the intermediate metabolite concentrations. The measurement function is a map to the values of the differential states and comprises measurements of metabolite concentrations. The differential equations are assumed to be fully known as standard mass action kinetics. An inequality path constraint is present (but potentially unknown in such settings) on the inner level and critical from a biological point of view: limitations due to molecular crowding impose an upper bound on the maximum total concentration of enzymes (controls) at any given time. Boundary conditions are fixed initial and terminal values of the metabolite concentrations.
are the final time and the time-integral of the intermediate metabolite concentrations. The measurement function is a map to the values of the differential states and comprises measurements of metabolite concentrations. The differential equations are assumed to be fully known as standard mass action kinetics. An inequality path constraint is present (but potentially unknown in such settings) on the inner level and critical from a biological point of view: limitations due to molecular crowding impose an upper bound on the maximum total concentration of enzymes (controls) at any given time. Boundary conditions are fixed initial and terminal values of the metabolite concentrations.
Mathematical formulation
The gIOC is given by
subject to
subject to
![\begin{array}{rcl}
\dot{x_1}(t) &=& \displaystyle 0 \\
\dot{x_2}(t) &=& \displaystyle p_1 \cdot x_1 \cdot u_1 - p_2 \cdot x_2 \cdot u_2 \\
\dot{x_3}(t) &=& \displaystyle p_2 \cdot x_2 \cdot u_2 - p_3 \cdot x_3 \cdot u_3 \\
\dot{x_4}(t) &=& \displaystyle p_3 \cdot x_3 \cdot u_3 \\
x(0) &=& (1, 0, 0, 0) \\
x_4(T) &=& 0.9 \\
x_i(t) &\ge& 0 \; \forall \; i \in \{1,2,3,4\} \\
u_i(t) &\in& [0,1] \; \forall \; i \in \{1,2,3\} \\
1 &\ge& u_1(t) + u_2(t) + u_3(t) \\
w_1, w_2 \in [0,1] \\
w_1 + w_2 = 1
\end{array}](https://mintoc.de/images/math/a/0/5/a05e3948b0c2afeb66859c9c787f9da0.png)
Here the four differential states and three control functions stand for the metabolite concentrations (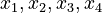 ) and the enzyme concentrations (
) and the enzyme concentrations (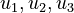 ). The two objective function candidates are the sum of intermediate metabolite concentrations and the transition time. The three model parameters
). The two objective function candidates are the sum of intermediate metabolite concentrations and the transition time. The three model parameters 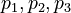 are kinetic parameters in mass action expressions.
are kinetic parameters in mass action expressions.
Data
The following table gives different values for 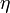 , componentwise for all four entries of
, componentwise for all four entries of 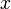 as time series, for different combinations of weights and noise levels that were used to produce the synthetic data via solution of forward optimal control problems.
as time series, for different combinations of weights and noise levels that were used to produce the synthetic data via solution of forward optimal control problems.
weights 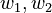
|
parameters 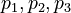
|
noise | number of time intervals 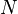
|
final time 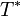
|
data 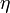
|
| [0.232, 0.768] | [1,1,1] | 0 | 20 | 4.3 |
[[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], [0, 0.215, 0.4298, 0.6446, 0.8593, 1.074, 1.2885, 1.503, 1.6591, 1.3381, 1.0792, 0.8704, 0.7021, 0.5662, 0.4849, 0.4846, 0.4844, 0.4842, 0.484, 0.4838, 0.4836], [0, 0.0, 0.0002, 0.0004, 0.0007, 0.001, 0.0015, 0.002, 0.0391, 0.36, 0.6186, 0.827, 0.9948, 1.1301, 1.1405, 0.92, 0.7423, 0.5989, 0.4832, 0.3899, 0.3147], [0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0001, 0.0004, 0.0008, 0.0013, 0.0019, 0.0729, 0.2935, 0.4715, 0.6152, 0.731, 0.8245, 0.9]] |
| [0.232, 0.768] | [1,1,1] | 0.2 | 20 | 4.3 |
[[1., 0.9590812,0.82266497,0.95877308,0.60614596,1.20781224, 0.92205471,1.0215116 ,0.89080449,1.05747735,1.04019676,1.06665347, 0.78545416,1.17084962,1.08658091,1.01467309,0.91098074,1.10349004, 0.83411596,0.73187308,0.70399766], [0.,0.37493181,0.10514573,0.79448823,0.44666767,1.19676033,1.14532119,1.64453389,1.93572019,1.37435635,0.92790967,1.11928728, 0.52061388,0.43837628,0.31518386,0.50300858,0.52891948,0.74255261, 0.07589526,0.64051491,0.47184952], [ 0., 0.23680072, 0.05047157,-0.03770305, 0.34603556,-0.45259701,0.25340369, 0.25177705, 0.16210031, 0.34367395, 0.96197961, 1.10224845, 1.21656021, 1.38442255, 1.02149302, 0.68818982, 0.7921558 , 0.32238544, 0.30229594, 0.43876605, 0.22073986], [ 0.,-0.01591557,-0.12432336,-0.17669569,-0.21325853,-0.2489822 , -0.22989873,-0.0564741 ,-0.19961696,-0.16036058,-0.04386598, 0.25004781, -0.07279584, 0.09573081,-0.12329308,-0.03451486, 0.0173815 , 0.79895333, 0.8178261 , 0.53498205, 1.1021996]] |
| [0,1] | [1,1,1] | 0 | 20 | 4.226 |
[[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0.211317, 0.422635, 0.633952, 0.845269, 1.05659, 1.2679, 1.47922, 1.69054, 1.90186, 1.95601, 1.58342, 1.2818, 1.03764, 0.839981, 0.685458, 0.685458, 0.685458, 0.685458, 0.685458, 0.685458], [0, 3.40252e-10, 2.02262e-09, 6.04129e-09, 1.32631e-08, 2.47434e-08, 4.23248e-08, 6.98021e-08, 1.16723e-07, 2.20847e-07, 0.103509, 0.476095, 0.777716, 1.02188, 1.21954, 1.36367, 1.10391, 0.893635, 0.72341, 0.58561, 0.474061], [0, 2.79389e-19, 2.05361e-18, 7.26553e-18, 1.82666e-17, 3.77412e-17, 6.87107e-17, 1.14894e-16, 1.82155e-16, 2.86358e-16, 3.73778e-11, 7.31532e-10, 5.75723e-09, 2.28945e-08, 7.3467e-08, 0.0103927, 0.270148, 0.480425, 0.65065, 0.78845, 0.9]] |
| [0,1] | [1,1,1] | 0.1 | 20 | 4.226 |
[[1.,0.98392517,1.02825092,1.0127091 ,1.21814838,1.03987996, 1.17367563,1.0721497 ,1.11254303,0.91560159,0.92664064,0.93069442, 1.01285111,1.10017347,0.9952073 ,1.05616016,1.12564585,1.02743444, 0.93306189,1.04808763,0.87659083], [0.,0.19112834,0.6016258 ,0.70894548,0.86077117,0.95316772, 1.12244906,1.51535841,1.48548905,1.87282215,2.13181979,1.48523121, 1.14624017,1.06839771,0.8838448 ,0.72466348,0.61379013,0.70096009, 0.73549769,0.62452413,0.61907767], [0., 0.04514029,-0.06510522,-0.00304812,-0.01620013, 0.006101, 0.04992798, 0.29317191, 0.11305888, 0.2285637 , 0.26142926, 0.50457228, 0.87829835, 0.90900075, 1.32279588, 1.42225272, 1.18086941, 0.67720058, 0.61562944, 0.6339817 , 0.36613472], [0.,-0.13882966, 0.18200648,-0.06629627,-0.01496019, 0.21349797,-0.10124824,-0.05505019, 0.23235014, 0.09448396, 0.06059911,-0.12137716, -0.00781841, 0.04355511, 0.1369212 ,-0.13011339, 0.2027646 , 0.51512985, 0.65331917, 0.78324169, 0.81304223]] |
Examples
The plots show noise free data for different weights from forward optimal control problems.
- Solution plots
References
| [Tsiantis2018] | Tsiantis, Nikolaos; Balsa-Canto, Eva; Banga, Julio R (2018): Optimality and identification of dynamic models in systems biology: an inverse optimal control framework. Bioinformatics, 34, 2433-2440 |  |