Difference between revisions of "Fuller's problem"

From mintOC
Jump to: navigation, search
m
(→‎Variants)
 
(31 intermediate revisions by 6 users not shown)
Line 6: Line 6:
 
}}
 
}}
  
−
The first control problem with an optimal [[:Category:Chattering|chattering]] solution was given by <bibref>Fuller1963</bibref>. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.
+
The first control problem with an optimal [[:Category:Chattering|chattering]] solution was given by <bib id="Fuller1963" />. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.
  
 
The mathematical equations form a small-scale [[:Category:ODE model|ODE model]]. The interior point equality conditions fix initial and terminal values of the differential states.
 
The mathematical equations form a small-scale [[:Category:ODE model|ODE model]]. The interior point equality conditions fix initial and terminal values of the differential states.
Line 14: Line 14:
 
For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by
 
For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by
  
 +
<p>
 
<math>
 
<math>
 
\begin{array}{llcl}
 
\begin{array}{llcl}
−
  \displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 \; \mathrm{d} t \\[1.5ex]
+
  \displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 & \; \mathrm{d} t \\[1.5ex]
−
  \mbox{s.t.} & \dot{x}_0(t) & = & x_1(t), \\
+
  \mbox{s.t.} & \dot{x}_0 & = & x_1, \\
−
  & \dot{x}_1(t) & = & 1 - 2 \; w(t), \\[1.5ex]
+
  & \dot{x}_1 & = & 1 - 2 \; w, \\[1.5ex]
 
  & x(0) &=& x_S, \\
 
  & x(0) &=& x_S, \\
 
  & x(t_f) &=& x_T, \\
 
  & x(t_f) &=& x_T, \\
Line 24: Line 25:
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
 +
</p>
  
 
== Parameters ==
 
== Parameters ==
Line 30: Line 32:
  
 
== Reference Solutions ==
 
== Reference Solutions ==
 +
 +
===Solutions obtained with jModelica===
 +
 +
The solution found for the relaxed Fuller's problem with jModelica using the solver Ipopt (with the linear solver MA27) is obtained with 12 iterations and the objective is 1.5296058259296967e-05.
 +
[[File:Fullerspng.png|left|200px|thumb|alt=a graph with the optimal solution of the Fuller's Problem with Optimica and Ipopt|Solution of the Fuller's Problem with Optimica and Ipopt]]
 +
<br  />
 +
<br style="clear:both;">
  
 
<!--
 
<!--
Line 41: Line 50:
 
-->
 
-->
  
−
== Source Code ==
+
== Variants ==
  
−
The differential equations in C code:
+
* Dropped terminal constraints with penalized deviation as additional Mayer term, see [[Fuller's initial value problem]],
−
<source lang="cpp">
+
* Several binary controls and dropped terminal constraints with penalized deviation as additional Mayer term, see [[Fuller's initial value multimode problem]],
 +
 
 +
== Source Code ==
  
−
</source>
+
* [[:Category:Muscod | Muscod code]] at [[Fuller's Problem (Muscod)]]
 +
* [[:Category:JModelica | JModelica code]] at [[Fuller's Problem (JModelica)]]
  
 
== Miscellaneous and further reading ==
 
== Miscellaneous and further reading ==
  
−
An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in <bibref>Zelikin1994</bibref>, a recent investigation of chattering controls in relay feedback systems in <bibref>Johansson2002</bibref>.
+
An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in <bib id="Zelikin1994" />, a recent investigation of chattering controls in relay feedback systems in <bib id="Johansson2002" />.
  
 
== References ==
 
== References ==
−
<bibreferences/>
+
<biblist />
  
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->

Latest revision as of 23:01, 8 January 2018

Fuller's problem
State dimension: 1
Differential states: 2
Discrete control functions: 1
Interior point equalities: 4


The first control problem with an optimal chattering solution was given by [Fuller1963]Author: A.T. Fuller
Journal: Journal of Electronics and Control
Pages: 63--71
Title: Study of an optimum nonlinear control system
Volume: 15
Year: 1963
Link to Google Scholar. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.

The mathematical equations form a small-scale ODE model. The interior point equality conditions fix initial and terminal values of the differential states.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 & \; \mathrm{d} t \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & x_1, \\ & \dot{x}_1 & = & 1 - 2 \; w, \\[1.5ex] & x(0) &=& x_S, \\ & x(t_f) &=& x_T, \\ & w(t) &\in& \{0, 1\}. \end{array}

Parameters

We use 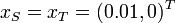x_S = x_T = (0.01, 0)^T.

Reference Solutions

Solutions obtained with jModelica

The solution found for the relaxed Fuller's problem with jModelica using the solver Ipopt (with the linear solver MA27) is obtained with 12 iterations and the objective is 1.5296058259296967e-05.

a graph with the optimal solution of the Fuller's Problem with Optimica and Ipopt
Solution of the Fuller's Problem with Optimica and Ipopt




Variants

Source Code

Miscellaneous and further reading

An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in [Zelikin1994]Address: Basel Boston Berlin
Author: Zelikin, M.I.; Borisov, V.F.
Publisher: Birkh\"auser
Title: Theory of chattering control with applications to astronautics, robotics, economics and engineering
Year: 1994
Link to Google Scholar, a recent investigation of chattering controls in relay feedback systems in [Johansson2002]Author: K.H. Johansson; Barabanov, A.E.; Astr\"om, K.J.
Journal: IEEE Transactions on Automatic Control
Number: 9
Pages: 1414--1423
Title: Limit Cycles with Chattering in Relay Feedback Systems
Volume: 47
Year: 2002
Link to Google Scholar.

References

There were no citations found in the article.

Retrieved from "https://mintoc.de/index.php?title=Fuller%27s_problem&oldid=2181"