Difference between revisions of "Oil Shale Pyrolysis"

From mintOC
Jump to: navigation, search
m
(→‎Mathematical formulation)
Line 13: Line 13:
  
 
<math>
 
<math>
−
\begin{array}{ll}
+
\begin{array}{lll}
−
  \displaystyle \min_{u} &  \displaystyle -x_1(t_N)^2  \\[1.5ex]
+
  \displaystyle \min_{u} &  \displaystyle &-x_1(t_N)^2  \\[1.5ex]
−
  \mbox{s.t.} &  \displaystyle \dot{x}_0(t) = -k_0x_0(t)-(k_2+k_3+k_4)x_0(t)x_1(t)\\
+
  \mbox{s.t.} &  \displaystyle \dot{x}_0 &= -k_0x_0-(k_2+k_3+k_4)x_0x_1\\
−
  &  \displaystyle \dot{x}_1(t) = k_0x_0(t)-k_1x_1(t) + k_2x_0(t)x_1(t)\\
+
  &  \displaystyle \dot{x}_1 &= k_0x_0-k_1x_1 + k_2x_0x_1\\
−
  &  \displaystyle k_i = a_i e^{-u(t)\frac{b_i}{R}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex]
+
  &  \displaystyle k_i &= a_i e^{-u\frac{b_i}{R}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex]
−
  &  \displaystyle t \in \left[t_0,t_N\right] \\
+
  &  \displaystyle t &\in \left[t_0,t_N\right] \\
−
  &  \displaystyle u(t) \in \left[698.15/748.15,1\right]\\
+
  &  \displaystyle u(t) &\in \left[698.15/748.15,1\right]\\
−
  &  \displaystyle x(t_0) = (1,0)^T\\
+
  &  \displaystyle x(t_0) &= (1,0)^T\\
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
Line 28: Line 28:
 
<math> u(t)= \frac{1}{u_{temp}} </math>, with  
 
<math> u(t)= \frac{1}{u_{temp}} </math>, with  
  
−
<math> u_{temp} \in \left[698.15,748.15\right] </math>  
+
<math> u_{temp} \in \left[698.15,748.15\right] </math>
  
 
== Parameters ==
 
== Parameters ==

Revision as of 17:05, 22 February 2016

Oil Shale Pyrolysis
State dimension: 1
Differential states: 2
Continuous control functions: 1
Discrete control functions: 0
Interior point equalities: 2


The following problem is an example from the global optimal control literature and was introduced in [Wen1977]The entry doesn't exist yet..


Mathematical formulation

\begin{array}{lll} \displaystyle \min_{u} & \displaystyle &-x_1(t_N)^2 \\[1.5ex] \mbox{s.t.} & \displaystyle \dot{x}_0 &= -k_0x_0-(k_2+k_3+k_4)x_0x_1\\ & \displaystyle \dot{x}_1 &= k_0x_0-k_1x_1 + k_2x_0x_1\\ & \displaystyle k_i &= a_i e^{-u\frac{b_i}{R}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex] & \displaystyle t &\in \left[t_0,t_N\right] \\ & \displaystyle u(t) &\in \left[698.15/748.15,1\right]\\ & \displaystyle x(t_0) &= (1,0)^T\\ \end{array}

where this is the normalized form with

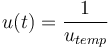u(t)= \frac{1}{u_{temp}} , with

u_{temp} \in \left[698.15,748.15\right]

Parameters

State variables
Symbol Initial value (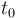t_0)
x_0(t) 1
x_1(t) 0
Parameters
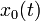
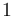
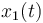
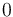
Symbol Value
a_1 8.86
a_2 24.25
a_3 23.67
a_4 18.75
a_5 20.7
b_1 20.3
b_2 37.4
b_3 33.8
b_4 28.2
b_5 31.0
Control variable
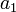
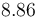
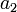
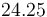
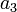
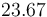
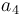
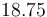
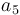
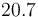
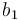
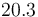
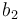
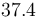
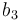
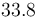
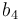
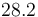
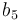
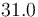
Symbol Interval
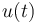
u(t) [698.15/748.15,1]

Measurement grid

Reference solution

Coming soon.

Source Code

Model descriptions are not yet available.

References

[Wen1977]The entry doesn't exist yet.
Retrieved from "https://mintoc.de/index.php?title=Oil_Shale_Pyrolysis&oldid=1722"