Oil Shale Pyrolysis
From mintOC
| Oil Shale Pyrolysis | |
|---|---|
| State dimension: | 4 |
| Differential states: | 4 |
| Continuous control functions: | 1 |
| Discrete control functions: | 0 |
| Path constraints: | 4 |
| Interior point equalities: | 0 |
The following problem is an example from the global optimal control literature and was introduced in [Wen1977]The entry doesn't exist yet.. The process starts with kerogen and is decomposed into pyrolytic bitumen, oil and gas, and residual carbon. The objective is to maximize the fraction of pyrolytic bitumen. There are 5 reactions including:
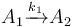
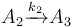
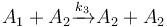
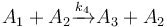
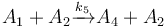
Each reaction is governed by a rate described by:
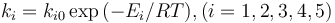
Mathematical formulation
![\begin{array}{lll}
\displaystyle \max_{T} & \displaystyle &x_2(t_N) \\[1.5ex]
\mbox{s.t.} & \displaystyle \dot{x}_1 &= -k_1x_1-(k_3+k_4+k_5)x_1x_2\\
& \displaystyle \dot{x}_2 &= k_1x_1-k_2x_2 + k_3x_1x_2\\
& \displaystyle \dot{x}_3 &= k_2x_2 + k_4x_1x_2\\
& \displaystyle \dot{x}_4 &= k_5x_1x_2\\
& \displaystyle k_i &= a_i e^{-\frac{b_i}{RT}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex]
& \displaystyle t &\in \left[t_0,t_N\right] \\
& \displaystyle T(t) &\in \left[698.15K,748.15K\right]\\
& \displaystyle x(t_0) &= (1,0,0,0)^T\\
\end{array}](https://mintoc.de/images/math/2/b/0/2b07ecd81011ae22420bbdafe9eaa73e.png)
Parameters
| Symbol | Initial value ( ) )
|
|
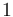
|
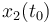
|
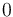
|
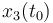
|
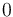
|
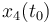
|
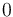
|
| Symbol | Value |
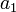
|
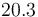
|
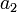
|
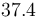
|
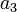
|
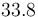
|
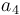
|
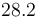
|
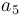
|
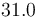
|
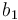
|
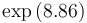
|
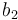
|
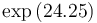
|
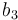
|
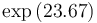
|
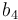
|
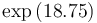
|
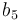
|
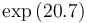
|
| Symbol | Interval |
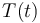
|
[698.15,748.15] |
Solutions
References
| [Wen1977] | The entry doesn't exist yet. |