Difference between revisions of "F-8 aircraft"
m (Added C code, progress) |
m |
||
| Line 30: | Line 30: | ||
<math>x_0</math> is the angle of attack in radians, <math>x_1</math> is the pitch angle, <math>x_2</math> is the pitch rate in rad/s, and the control function <math>w = w(t)</math> is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>. | <math>x_0</math> is the angle of attack in radians, <math>x_1</math> is the pitch angle, <math>x_2</math> is the pitch rate in rad/s, and the control function <math>w = w(t)</math> is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>. | ||
| + | |||
| + | The control w(t) is restricted to take values from a finite set only. However, as w(t) enters | ||
== Initial and terminal values == | == Initial and terminal values == | ||
| Line 58: | Line 60: | ||
The differential equations in C code: | The differential equations in C code: | ||
<source lang="cpp"> | <source lang="cpp"> | ||
| + | double x1 = xd[0]; | ||
| + | double x2 = xd[1]; | ||
| + | double x3 = xd[2]; | ||
| − | + | double u0 = -0.05236; | |
| − | + | double u1 = 0.05236; | |
| − | + | double f00, f10, f20; | |
| − | + | double f01, f11, f21; | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | f00 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2 | |
| − | + | - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u0 + 0.28*x1*x1*u0 + 0.47*x1*u0*u0 + 0.63*u0*u0*u0; | |
| − | + | f10 = x3; | |
| − | + | f20 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1 | |
| − | + | - 20.967*u0 + 6.265*x1*x1*u0 + 46*x1*u0*u0 + 61.4*u0*u0*u0; | |
| − | + | f01 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2 | |
| − | + | - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u1 + 0.28*x1*x1*u1 + 0.47*x1*u1*u1 + 0.63*u1*u1*u1; | |
| − | + | f11 = x3; | |
| − | + | f21 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1 | |
| − | + | -20.967*u1 + 6.265*x1*x1*u1 + 46*x1*u1*u1 + 61.4*u1*u1*u1; | |
| − | + | rhs[0] = u[0]*f01 + (1-u[0])*f00; | |
| − | + | rhs[1] = u[0]*f11 + (1-u[0])*f10; | |
| − | + | rhs[2] = u[0]*f21 + (1-u[0])*f20; | |
</source> | </source> | ||
Revision as of 00:39, 1 November 2008
| F-8 aircraft | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Discrete control functions: | 1 |
| Interior point equalities: | 6 |
The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by Kaya and Noakes in 2003<bibref>Kaya2003</bibref> and aims at controlling an aircraft in a time-optimal way from an initial state to a terminal state.
The mathematical equations form a small-scale ODE Model. The interior point equality conditions fix both initial and terminal values of the differential states.
The optimal integer control functions shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.
Contents
Mathematical formulation
For ![t \in [0, T]](https://mintoc.de/images/math/e/6/6/e66a2b7fedcba80ccb192b87440f8d9c.png)
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w, T} & T \\[1.5ex]
\mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 \\
&&& + 3.846 \; x_0^3 - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\
& \dot{x}_1 &=& x_2 \\
& \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\
& x(0) &=& x_0, \\
& x(T) &=& x_T, \\
& w(t) &\in& \{-0.05236,0.05236\}.
\end{array}](https://mintoc.de/images/math/3/d/4/3d414a7aac0303b674e74c1c07b48ec2.png)
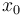is the angle of attack in radians, 
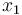is the pitch angle, 
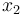is the pitch rate in rad/s, and the control function 
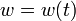is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>.
The control w(t) is restricted to take values from a finite set only. However, as w(t) enters
Initial and terminal values
Both initial as terminal values of the differential states are fixed.
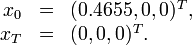
Reference solutions
The optimal objective value of this problem given in Sager 2005<bibref>Sager2005</bibref> is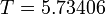 
.
- Reference solution plots
Optimal relaxed control on a coarse control discretization grid and corresponding differential states.
Optimal relaxed control on a fine control discretization grid and corresponding differential states.
Optimal integer control and corresponding differential states.
Source Code
C
The differential equations in C code:
double x1 = xd[0]; double x2 = xd[1]; double x3 = xd[2]; double u0 = -0.05236; double u1 = 0.05236; double f00, f10, f20; double f01, f11, f21; f00 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2 - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u0 + 0.28*x1*x1*u0 + 0.47*x1*u0*u0 + 0.63*u0*u0*u0; f10 = x3; f20 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1 - 20.967*u0 + 6.265*x1*x1*u0 + 46*x1*u0*u0 + 61.4*u0*u0*u0; f01 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2 - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u1 + 0.28*x1*x1*u1 + 0.47*x1*u1*u1 + 0.63*u1*u1*u1; f11 = x3; f21 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1 -20.967*u1 + 6.265*x1*x1*u1 + 46*x1*u1*u1 + 61.4*u1*u1*u1; rhs[0] = u[0]*f01 + (1-u[0])*f00; rhs[1] = u[0]*f11 + (1-u[0])*f10; rhs[2] = u[0]*f21 + (1-u[0])*f20;
Miscellaneous and Further Reading
See <bibref>Kaya2003</bibref> and <bibref>Sager2005</bibref> for details.
References
<bibreferences/>
