F-8 aircraft
| F-8 aircraft | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Discrete control functions: | 1 |
| Path constraints: | 2 |
| Interior point equalities: | 6 |
The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by Kaya and Noakes and aims at controlling an aircraft in a time-optimal way from an initial state to a terminal state.
The mathematical equations form a small-scale ODE model. The interior point equality conditions fix both initial and terminal values of the differential states.
The optimal, relaxed control function shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.
Contents
[hide]Mathematical formulation
For ![t \in [0, T]](https://mintoc.de/images/math/e/6/6/e66a2b7fedcba80ccb192b87440f8d9c.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w, T} & T \\[1.5ex]
\mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\
&&& - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\
& \dot{x}_1 &=& x_2 \\
& \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\
&&& - 20.967 \; w + 6.265 \; x_0^2 \; w + 46 \; x_0 \; w^2 + 61.4 \; w^3 \\
& x(0) &=& (0.4655,0,0)^T, \\
& x(T) &=& (0,0,0)^T, \\
& w(t) &\in& \{-0.05236,0.05236\}.
\end{array}](https://mintoc.de/images/math/d/2/b/d2bd7e6d1cc8affb72d59248a105d528.png)
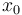 is the angle of attack in radians,
is the angle of attack in radians, 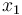 is the pitch angle,
is the pitch angle, 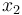 is the pitch rate in rad/s, and the control function
is the pitch rate in rad/s, and the control function 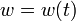 is the tail deflection angle in radians. This model goes back to Garrard[Garrard1977]Author: Garrard, W.L.; Jordan, J.M.
is the tail deflection angle in radians. This model goes back to Garrard[Garrard1977]Author: Garrard, W.L.; Jordan, J.M.
Journal: Automatica
Pages: 497--505
Title: Design of Nonlinear Automatic Control Systems
Volume: 13
Year: 1977 .
.
In the control problem, both initial and terminal values of the differential states are fixed.
Reformulation
The control w(t) is restricted to take values from a finite set only. Hence, the control problem can be reformulated equivalently to
![\begin{array}{llcl}
\displaystyle \min_{x, w, T} & T \\[1.5ex]
\mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\
&&& - \left( 0.215 \; \xi - 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 - 0.63 \; \xi^3 \right) \; w \\
&&& - \left( - 0.215 \; \xi + 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 + 0.63 \; \xi^3 \right) \; (1 - w) \\
& &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\
&&& + 0.215 \; \xi - 0.28 \; x_0^2 \; \xi + 0.47 \; x_0 \; \xi^2 - 0.63 \; \xi^3 \\
&&& - \left( 0.215 \; \xi - 0.28 \; x_0^2 \; \xi - 0.63 \; \xi^3 \right) \; 2 w \\
& \dot{x}_1 &=& x_2 \\
& \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\
&&& - \left( 20.967 \; \xi - 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 - 61.4 \; \xi^3 \right) \; w \\
&&& - \left( - 20.967 \; \xi + 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 + 61.4 \; \xi^3 \right) \; (1 - w) \\
& &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\
&&& + 20.967 \; \xi - 6.265 \; x_0^2 \; \xi + 46 \; x_0 \; \xi^2 - 61.4 \; \xi^3 \\
&&& - \left( 20.967 \; \xi - 6.265 \; x_0^2 \; \xi - 61.4 \; \xi^3 \right) \; 2 w \\
& x(0) &=& (0.4655,0,0)^T, \\
& x(T) &=& (0,0,0)^T, \\
& w(t) &\in& \{0,1\},
\end{array}](https://mintoc.de/images/math/0/4/a/04a0e56e2d185c764c658785ce00ade8.png)
with 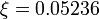 . Note that there is a bijection between optimal solutions of the two problems.
. Note that there is a bijection between optimal solutions of the two problems.
Reference solutions
We provide here a comparison of different solutions reported in the literature. The numbers show the respective lengths 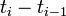 of the switching arcs with the value of
of the switching arcs with the value of 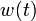 on the upper or lower bound (given in the second column). Claim denotes what is stated in the respective publication, Simulation shows values obtained by a simulation with a Runge-Kutta-Fehlberg method of 4th/5th order and an integration tolerance of
on the upper or lower bound (given in the second column). Claim denotes what is stated in the respective publication, Simulation shows values obtained by a simulation with a Runge-Kutta-Fehlberg method of 4th/5th order and an integration tolerance of 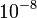 .
.
| Arc | w(t) | Lee et al.[Lee1997a]Author: Lee, H.W.J.; Teo, K.L.; Rehbock, V.; Jennings, L.S. Journal: Dynamic Systems and Applications Pages: 243--262 Title: Control Parametrization Enhancing Technique for Time-Optimal Control Problems Volume: 6 Year: 1997  |
Kaya[Kaya2003]Author: C.Y. Kaya; J.L. Noakes Journal: Journal of Optimization Theory and Applications Pages: 69--92 Title: A Computational Method for Time-Optimal Control Volume: 117 Year: 2003  |
Sager[Sager2005]Address: Tönning, Lübeck, Marburg Author: S. Sager Editor: ISBN 3-89959-416-9 Publisher: Der andere Verlag Title: Numerical methods for mixed--integer optimal control problems Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf Year: 2005  |
Schlueter/ Gerdts | Sager |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.00000 | 0.10292 | 0.10235 | 0.0 | 1.13492 |
| 2 | 0 | 2.18800 | 1.92793 | 1.92812 | 0.608750 | 0.34703 |
| 3 | 1 | 0.16400 | 0.16687 | 0.16645 | 3.136514 | 1.60721 |
| 4 | 0 | 2.88100 | 2.74338 | 2.73071 | 0.654550 | 0.69169 |
| 5 | 1 | 0.33000 | 0.32992 | 0.32994 | 0.0 | 0.0 |
| 6 | 0 | 0.47200 | 0.47116 | 0.47107 | 0.0 | 0.0 |
| Claim: Infeasibility | - | 1.00E-10 | 7.30E-06 | 5.90E-06 | 3.29169e-06 | 2.21723e-07 |
| Claim: Objective | - | 6.03500 | 5.74217 | 5.72864 | 4.39981 | 3.78086 |
| Simulation: Infeasibility | - | 1.75E-03 | 1.64E-03 | 5.90E-06 | 3.29169e-06 | 2.21723e-07 |
| Simulation: Objective | - | 6.03500 | 5.74218 | 5.72864 | 4.39981 | 3.78086 |
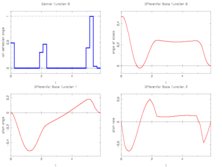
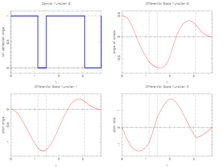
The best known optimal objective value of this problem given is given by 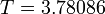 . The corresponding solution is shown in the rightmost plot. The solution of bang-bang type switches three times, starting with
. The corresponding solution is shown in the rightmost plot. The solution of bang-bang type switches three times, starting with 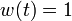 .
.
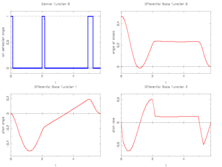
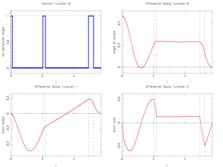
- Reference solution plots
Integer control and corresponding differential states from Sager[Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005 .
.
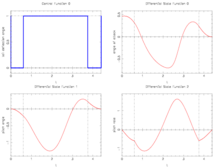
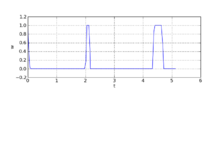
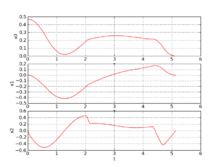
jModelica
Objective : 5.12799232 infeasibility : 6.2235588037251599e-10
- Obtained solution plots
Source Code
Model descriptions are available in
- AMPL code at F-8 aircraft (AMPL)
- Muscod code at F-8 aircraft (Muscod)
- JModelica code at F-8 aircraft (JModelica)
Variants
- a prescribed time grid for the control function, see F-8 aircraft (AMPL),
Miscellaneous and Further Reading
See [Kaya2003]Author: C.Y. Kaya; J.L. Noakes
Journal: Journal of Optimization Theory and Applications
Pages: 69--92
Title: A Computational Method for Time-Optimal Control
Volume: 117
Year: 2003 and [Sager2005]Address: Tönning, Lübeck, Marburg
and [Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005 for details.
for details.
References
| [Garrard1977] | Garrard, W.L.; Jordan, J.M. (1977): Design of Nonlinear Automatic Control Systems. Automatica, 13, 497--505 |  |
| [Kaya2003] | C.Y. Kaya; J.L. Noakes (2003): A Computational Method for Time-Optimal Control. Journal of Optimization Theory and Applications, 117, 69--92 |  |
| [Lee1997a] | Lee, H.W.J.; Teo, K.L.; Rehbock, V.; Jennings, L.S. (1997): Control Parametrization Enhancing Technique for Time-Optimal Control Problems. Dynamic Systems and Applications, 6, 243--262 |  |
| [Sager2005] | S. Sager (2005): Numerical methods for mixed--integer optimal control problems. (%edition%). Der andere Verlag, Tönning, Lübeck, Marburg, %pages% |  |