F-8 aircraft (AMPL)
This page contains a discretized version of the MIOCP F-8 aircraft in AMPL format. Note however that it has been slightly reformulated to serve as a benchmark for MINLP solvers. You should be aware of the comments regarding discretization made on the AMPL overview page. Note that you will need to include two generic support AMPL files, ampl_general.mod and ampl_general.dat.
Contents
[hide]Model
The main difficulty in calculating a time-optimal solution for the F-8 aircraft problem is the determination of the correct switching structure and of the switching points.
If we want to formulate a MINLP, we have to slightly modify this problem. Our aim is not a minimization of the overall time, but now we want to get as close as possible to the origin (0,0,0) in
a prespecified time 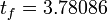 on an equidistant time grid. As this time grid is not a superset of the one used for the time-optimal solution, one can not expect to reach the target state exactly.
on an equidistant time grid. As this time grid is not a superset of the one used for the time-optimal solution, one can not expect to reach the target state exactly.
AMPL
The model in AMPL code for a fixed control discretization grid with a collocation method. We need a model file f8_ampl.mod,
# -------------------------------------------------------------- # F-8 aircraft control problem with collocation (implicit Euler) # (c) Sebastian Sager # -------------------------------------------------------------- var x {I, 1..nx}; param xi > 0; minimize Deviation: sum {i in 1..3} x[nt,i]*x[nt,i]; subj to ODE_DISC_1 {i in I diff {0}}: x[i,1] = x[i-1,1] + (dt[uidx[i]]/ntperu) * ( - 0.877*x[i,1] + x[i,3] - 0.088*x[i,1]*x[i,3] + 0.47*x[i,1]*x[i,1] - 0.019*x[i,2]*x[i,2] - x[i,1]*x[i,1]*x[i,3] + 3.846*x[i,1]*x[i,1]*x[i,1] + 0.215*xi - 0.28*x[i,1]*x[i,1]*xi + 0.47*x[i,1]*xi^2 - 0.63*xi^2 - 2*w[uidx[i]] * ( 0.215*xi - 0.28*x[i,1]*x[i,1]*xi - 0.63*xi^3 ) ); subj to ODE_DISC_2 {i in I diff {0}}: x[i,2] = x[i-1,2] + (dt[uidx[i]]/ntperu) * x[i,3]; subj to ODE_DISC_3 {i in I diff {0}}: x[i,3] = x[i-1,3] + (dt[uidx[i]]/ntperu) * ( - 4.208*x[i,1] - 0.396*x[i,3] - 0.47*x[i,1]*x[i,1] - 3.564*x[i,1]*x[i,1]*x[i,1] + 20.967*xi - 6.265*x[i,1]*x[i,1]*xi + 46*x[i,1]*xi^2 - 61.4*xi^3 - 2*w[uidx[i]] * (20.967*xi - 6.265*x[i,1]*x[i,1]*xi - 61.4*xi^3) );
a data file f8_ampl.dat,
# Algorithmic parameters param ntperu := 500; param nu := 60; param nt := 30000; param nx := 3; param fix_w := 0; param fix_dt := 1; # Problem parameters param xi := 0.05236; param T := 8; # Initial values differential states let x[0,1] := 0.4655; let x[0,2] := 0.0; let x[0,3] := 0.0; for {i in 1..3} { fix x[0,i]; } # Initial values control let {i in U} w[i] := 0.0; for {i in 0..(nu-1) / 2} { let w[i*2] := 1.0; } let {i in U} dt[i] := 3.78086 / nu;
and a running script f8_ampl.run,
model ampl_general.mod; model ampl_f8.mod; data ampl_f8.dat; data ampl_general.dat; option presolve_eps 1e-10; option solver ...; solve; param myt; let myt := 0; for {i in I} { if ( dt[uidx[i]] > 1e-6 ) then { print myt, w[uidx[i]], x[i,1], x[i,2] > resultInt.txt; } let myt := myt + (dt[uidx[i]]/ntperu); } display w;
Results
Bonmin
The solution calculated by Bonmin (subversion revision number 1453, default settings, 3 GHz, Linux 2.6.28-13-generic, with ASL(20081205)) has an objective function value of 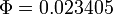 , while the optimum of the relaxation is
, while the optimum of the relaxation is 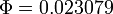 . Bonmin needs 85702 iterations and 7031 nodes (64282 seconds). Strong branching is done 45 times (1212 iterations), with 0 fathomed nodes and 4 fixed variables. The intervals on the equidistant grid on which
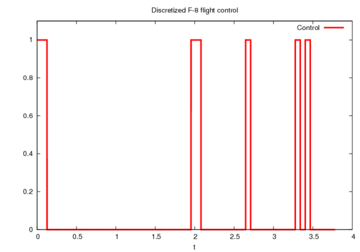
. Bonmin needs 85702 iterations and 7031 nodes (64282 seconds). Strong branching is done 45 times (1212 iterations), with 0 fathomed nodes and 4 fixed variables. The intervals on the equidistant grid on which 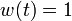 holds, counting from 0 to 59, are 0, 1, 31, 32, 42, 52, and 54.
holds, counting from 0 to 59, are 0, 1, 31, 32, 42, 52, and 54.
Knitro
A solution obtained by Knitro version 6.0 under NEOS server environment was tested by Henry Kar Ming Chan for the reduced model. The reduced model is defined by using less number of period of time (i.e. ntperu := 200). The standard defaults were used except the strong branching strategies, the integrality gap tolerances and maximum nodes without parallel features. Final objective value is 0.02200987541. Number of nodes processed is 861 and number of subproblems solved is 872. Total program CPU time is 10775.09 seconds with time spent in evaluations for 3276.315 seconds. The intervals on the equidistant grid on which 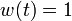 holds, counting from 0 to 59, are 0, 1, 31, 32, 42, 52, and 54.
holds, counting from 0 to 59, are 0, 1, 31, 32, 42, 52, and 54.
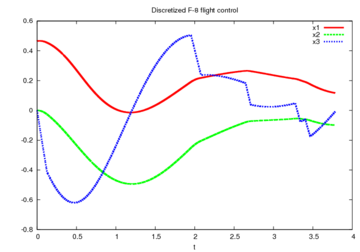
- Reference solution plots
Comparing this solution to the ones described for F-8 aircraft, this solution might well not be the global optimum.