Difference between revisions of "Hanging chain problem"
From mintOC
FelixMueller (Talk | contribs) (→Mathematical formulation) |
FelixMueller (Talk | contribs) (→Mathematical formulation) |
||
| Line 20: | Line 20: | ||
\mbox{s.t.} & \dot{x}_1 & = & u, \\ | \mbox{s.t.} & \dot{x}_1 & = & u, \\ | ||
& \dot{x}_2 & = & x_1 (1+u^2)^{1/2}, \\ | & \dot{x}_2 & = & x_1 (1+u^2)^{1/2}, \\ | ||
| − | & \dot{x}_3 & = & (1+u^2)^{1/2), \\ | + | & \dot{x}_3 & = & (1+u^2)^{1/2}, \\ |
| + | & x(t_0) &=& (a,0,0)^T, \\ | ||
| + | & x_1(t_f) &=& b, \\ | ||
| + | & x_3(t_f) &=& Lp, \\ | ||
| + | & x(t) &\in& [0,10], \\ | ||
| + | & u(t) &\in& [-10,20]. | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
Revision as of 18:41, 5 May 2016
| Hanging chain problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point equalities: | 2 |
The Hanging chain problem is concerned with finding a chain (of uniform density) of length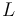 
suspendend between two points 
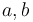with minimal potential energy. (Problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, u} & x_2(t_f) \\[1.5ex]
\mbox{s.t.} & \dot{x}_1 & = & u, \\
& \dot{x}_2 & = & x_1 (1+u^2)^{1/2}, \\
& \dot{x}_3 & = & (1+u^2)^{1/2}, \\
& x(t_0) &=& (a,0,0)^T, \\
& x_1(t_f) &=& b, \\
& x_3(t_f) &=& Lp, \\
& x(t) &\in& [0,10], \\
& u(t) &\in& [-10,20].
\end{array}](https://mintoc.de/images/math/b/c/7/bc780667f14aed98c5f25693189fe3bb.png)
Parameters
In this model the parameters used are \begin{array}{rcl} [t_0, t_f] &=& [0, 1],\\ (a,b) &=& (0.4, 0.2),\\ Lp &=& 4. \end{array}
Source Code
Model descriptions are available in
