Difference between revisions of "D'Onofrio chemotherapy model"

D'Onofrio chemotherapy model
State dimension:	1
Differential states:	4
Continuous control functions:	2

Revision as of 23:07, 27 June 2016

This cancer chemotherapy model is based on the work of d'Onofrio. The corresponding dynamic describes the effect of two different drugs administered to the patient. An anti-angiogetic drug is used to suppress the formation of blood vessels from existing vessels and thereby starving the tumors supply of proliferating vessels. In addition a cytostatic drug effects the proliferation of the tumor cells directly. The dynamic of the problem is given by an ODE model.

Mathematical formulation

For $t \in [t_0, t_f]$ the optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, u} & x_0(t_f) &+& \alpha \int_{t_0}^{t_f} u_0(t)^2 \text{d}t \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & - \zeta x_0 \text{ln} \left( \frac{x_0}{x_1} \right) - F \; x_0 u_1, \\ & \dot{x}_1 & = & b x_0 - \mu x_1 - d x_0^{\frac{2}{3}}x_1 - G u_0 x_1 - \eta x_1 u_1, \\ & \dot{x}_2 & = & u_0, \\ & \dot{x}_3 & = & u_1, \\ [1.5ex] & 0 & \leq & u_0 \quad \leq u_0^{max}, \\ & 0 & \leq & u_1 \quad \leq u_1^{max}, \\ & u_0 & \in & [0,u_0^{max}],\\ & u_1 & \in & [0,u_1^{max}],\\ & x_2 & \leq & x_2^{max}, \\ & x_3 & \leq & x_3^{max}. \end{array}$

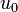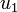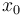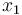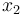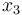where the control $u_0$ denotes the administered amount of anti-angiogetic drugs and $u_1$ the amount of cytostatic drugs. The state $x_0$ describes the volume of tumor and $x_1$ the volume of neighboring blood vessels. The remaining states $x_2$ and $x_3$ are used to constraint the maximum amount of drugs over the duration of the therapy.

Parameters

In the model these parameters are fixed.

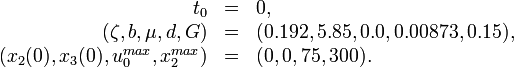
$\begin{array}{rcl} t_0 &=& 0,\\ (\zeta, b, \mu, d, G) &=& (0.192, 5.85, 0.0, 0.00873, 0.15),\\ (x_2(0), x_3(0), u_0^{max}, x_2^{max}) &=& (0,0,75,300). \end{array}$

The parameters 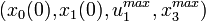$(x_0(0), x_1(0), u_1^{max}, x_3^{max})$ can be taken from the parameter sets shown in the following section. To the remaining parameters 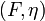$(F, \eta)$ exists no experimental data.

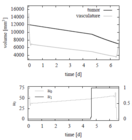
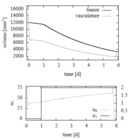
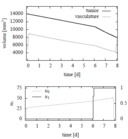
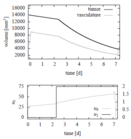
Reference Solutions

The problem can be solved with the [multiple shooting method]. For the following solutions the control functions and states are discretized on the same grid, with 100 nodes. The unknown parameters are chosen from the following parameter sets

Parameter set 1

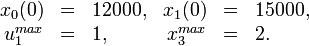
$\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}$

Parameter set 2

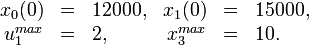
$\begin{array}{rclrcl} x_0(0) &=& 12000,& x_1(0) &=& 15000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}$

Parameter set 3

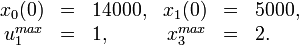
$\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 1,& x_3^{max} &=& 2.\\ \end{array}$

Parameter set 4

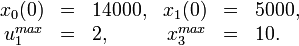
$\begin{array}{rclrcl} x_0(0) &=& 14000,& x_1(0) &=& 5000,\\ u_1^{max} &=& 2,& x_3^{max} &=& 10.\\ \end{array}$

Furthermore in the objective function 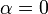$\alpha =0$ is chosen.

Reference solution plots
Optimal controls and states computed with a multiple shooting approach on the same discretization grid with 100 nodes and parameter set 1.
Optimal controls and states with parameter set 2.
Optimal controls and states with parameter set 3.
Optimal controls and states with parameter set 4.

Source Code

Muscod code at D'Onofrio chemotherapy model (Muscod)

References

There were no citations found in the article.

Difference between revisions of "D'Onofrio chemotherapy model"

Revision as of 23:07, 27 June 2016

Contents

Mathematical formulation

Parameters

Reference Solutions

Source Code

References

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Support

Tools

@@ Line 21: / Line 21: @@
               & 0 & \leq & u_0 \quad \leq  u_0^{max},  \\
               & 0 & \leq & u_1 \quad  \leq u_1^{max}, \\
+             & u_0 & \in & [0,u_0^{max}],\\
+             & u_1 & \in & [0,u_1^{max}],\\
               & x_2 & \leq & x_2^{max},  \\
               & x_3 & \leq & x_3^{max}.