Difference between revisions of "Control of Transmission Lines"

From mintOC
Jump to: navigation, search
(Mathematical formulation.)
(Parameters, Discretization, Source Code)
Line 6: Line 6:
 
<p>
 
<p>
 
<math>
 
<math>
−
\partial_t \xi_r(x,t) + \Lambda \xi_r(x,t) + B \xi_r(x,t) = 0,
+
\partial_t \xi_r(x,t) + \Lambda_r \xi_r(x,t) + B_r \xi_r(x,t) = 0,
 
</math>
 
</math>
 
</p>
 
</p>
−
with a diagonal 2x2-matrix <math>\Lambda</math> and a symmetric matrix <math>B</math>. We combine all <math>m</math> single line states to a large state vector <math>\boldsymbol{\xi}(x,t)</math> to obtain the system
+
with a diagonal 2x2-matrix <math>\Lambda_r</math> and a symmetric matrix <math>B_r</math>. We combine all <math>m</math> single line states to a large state vector <math>\boldsymbol{\xi}(x,t)</math> to obtain the system
 
<p>
 
<p>
 
<math>
 
<math>
Line 37: Line 37:
 
<p>
 
<p>
 
<math>
 
<math>
−
   \displaystyle \min_{\boldsymbol{u} \in \mathcal{U}} \frac{1}{2}\sum_{s \in V_S} \int_0^{T} \left( Q_s(t) - \sum_{r \in \delta_{s}} \xi_r^+(l_r,t) \right)^2 dt,
+
   \displaystyle \min_{\boldsymbol{v} \in \mathcal{V}, \boldsymbol{u} \in \mathcal{U}} \frac{1}{2}\sum_{s \in V_S} \int_0^{T} \left( Q_s(t) - \sum_{r \in \delta_{s}} \xi_r^+(l_r,t) \right)^2 dt,
 
</math>
 
</math>
 
</p>
 
</p>
Line 43: Line 43:
  
 
== Parameters ==
 
== Parameters ==
 +
 +
A detailed account of the network structures and parameter settings can be found in <bib id="Goettlich2018" /> and in the source code below.
  
 
== Discretization ==
 
== Discretization ==
 +
 +
The mixed-integer variables <math>\boldsymbol{v}(t)</math> are transcribed via Partial Outer Convexification and the dynamics are discretized using Finite Volumes with upwind fluxes for the characteristic variables and explicit first-order time-stepping.
  
 
== Reference Solution ==
 
== Reference Solution ==
  
 
==Source Code==
 
==Source Code==
 +
 +
The C++ code for the results in the paper are not publicly available, but a more user-friendly Python/CasADi-Version is available on [https://github.com/apotschka/poc-transmission-lines GitHub/poc-transmission-lines].
  
 
==References==
 
==References==

Revision as of 15:11, 12 September 2018

This problem was provided by Göttlich, Potschka, and Teuber [Goettlich2018]Author: G{\"o}ttlich, Simone; Potschka, Andreas; Teuber, Claus
Institution: University of Mannheim
Note: Optimization Online 6312
Title: A partial outer convexification approach to control transmission lines
Url: http://www.optimization-online.org/DB_HTML/2017/11/6312.html
Year: 2018
Link to Google Scholar. It is governed by a 2x2-system of conservation laws based on the telegraph equations for single transmission lines, which are then connected to form a network. The objective is to minimize the quadratic deviation of the load delivered to customer nodes from their demand by continuously controlling the power inflow to the network at the energy producer nodes and by discrete but time-varying switches at the coupling nodes inside the network.

Mathematical formulation

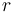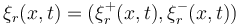The dynamics on the r-th transmission line with spatial variable x \in [0, l_r], temporal variable t \in [0, T], and state variable \xi_r(x,t) = (\xi^+_r(x, t), \xi^-_r(x, t)) containing the characteristic variables for right-traveling and left-traveling components are given by the hyperbolic PDE system

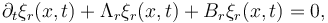
\partial_t \xi_r(x,t) + \Lambda_r \xi_r(x,t) + B_r \xi_r(x,t) = 0,

with a diagonal 2x2-matrix 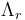\Lambda_r and a symmetric matrix 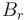B_r. We combine all 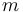m single line states to a large state vector 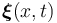\boldsymbol{\xi}(x,t) to obtain the system

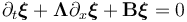
\partial_t \boldsymbol{\xi} + \boldsymbol{\Lambda} \partial_x \boldsymbol{\xi} + \mathbf{B} \boldsymbol{\xi} = 0

and formulate the coupling between the lines and the continuously controlled power inflow 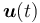\boldsymbol{u}(t) as boundary conditions involving distribution matrices 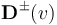\mathbf{D}^\pm(v), which depend on a discrete switching signal 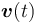\boldsymbol{v}(t), and constant distribution matrices 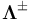\mathbf{\Lambda}^\pm of size m \times m according to

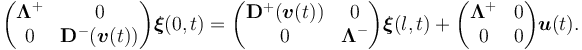
\begin{pmatrix} \boldsymbol{\Lambda}^+ & 0\\ 0 & \mathbf{D}^-(\boldsymbol{v}(t)) \end{pmatrix} \boldsymbol{\xi}(0,t) = \begin{pmatrix} \mathbf{D}^+(\boldsymbol{v}(t)) & 0\\ 0 & \boldsymbol{\Lambda}^- \end{pmatrix} \boldsymbol{\xi}(l,t) + \begin{pmatrix} \boldsymbol{\Lambda}^+ & 0\\ 0 & 0 \end{pmatrix} \boldsymbol{u}(t).

The continuous control 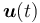\boldsymbol{u}(t) is subject to simple bounds.

The objective is to track the given demands 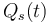Q_s(t) of consumers, which can be formulated as

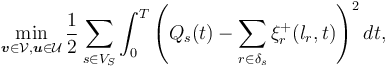
\displaystyle \min_{\boldsymbol{v} \in \mathcal{V}, \boldsymbol{u} \in \mathcal{U}} \frac{1}{2}\sum_{s \in V_S} \int_0^{T} \left( Q_s(t) - \sum_{r \in \delta_{s}} \xi_r^+(l_r,t) \right)^2 dt,

where 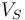V_S is the set of consumer nodes and 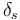\delta_s is the set of all lines adjacent to vertex s.

Parameters

A detailed account of the network structures and parameter settings can be found in [Goettlich2018]Author: G{\"o}ttlich, Simone; Potschka, Andreas; Teuber, Claus
Institution: University of Mannheim
Note: Optimization Online 6312
Title: A partial outer convexification approach to control transmission lines
Url: http://www.optimization-online.org/DB_HTML/2017/11/6312.html
Year: 2018
Link to Google Scholar and in the source code below.

Discretization

The mixed-integer variables 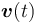\boldsymbol{v}(t) are transcribed via Partial Outer Convexification and the dynamics are discretized using Finite Volumes with upwind fluxes for the characteristic variables and explicit first-order time-stepping.

Reference Solution

Source Code

The C++ code for the results in the paper are not publicly available, but a more user-friendly Python/CasADi-Version is available on GitHub/poc-transmission-lines.

References

[Goettlich2018]G{\"o}ttlich, Simone; Potschka, Andreas; Teuber, Claus (2018): A partial outer convexification approach to control transmission lines. University of Mannheim.Link to Google Scholar
Retrieved from "https://mintoc.de/index.php?title=Control_of_Transmission_Lines&oldid=2240"