Difference between revisions of "Lotka Volterra fishing problem (Julia Neural Network solve)"
From mintOC
ClemensZeile (Talk | contribs) (Created page with "This is an implementation of the Lotka Volterra fishing problem using Julia and a neural network by Julius Martensen, see https://github.com/AlCap23/IMPRS2021 The control...") |
ClemensZeile (Talk | contribs) |
||
| Line 84: | Line 84: | ||
</source> | </source> | ||
| + | <gallery caption="Reference solution plot" widths="280px" heights="240px" perrow="1"> | ||
| + | Image:Lotka volterra optimal control julia NN.gif| Animated solution process | ||
| + | </gallery> | ||
[[Category: Julia/JuMP]] | [[Category: Julia/JuMP]] | ||
Latest revision as of 17:20, 20 September 2021
This is an implementation of the Lotka Volterra fishing problem using Julia and a neural network by Julius Martensen, see https://github.com/AlCap23/IMPRS2021
The control function was relaxed, i.e. ![u(t) \in [0,1]](https://mintoc.de/images/math/b/e/f/bef45f7df7f2ba2926be25e8a2e4f43e.png) .
.
using LinearAlgebra using Plots using OrdinaryDiffEq using Flux using DiffEqFlux # Example for optimal control controller = Chain(Dense(1, 10, relu), Dense(10,10, relu), Dense(10,10, relu), Dense(10, 1, σ)) pnn, f = Flux.destructure(controller) function lotka!(du, u, p, t) c = f(p)([t])[1] du[1] = (1-0.4*c)*u[1] - u[1]*u[2] du[2] = u[1]*u[2] - (1+0.2*c)*u[2] du[3] = (u[1] - 1)^2 + (u[2] -1)^2 end u0 = Float32[0.5; 0.7; 0.0] tspan = (0.0f0, 12.0f0) Δt = 12.0f0/100 prob = ODEProblem(lotka!, u0, tspan, pnn) solution = solve(prob, Tsit5(), saveat = Δt) length(solution) function loss(p) s_ = solve(prob, Tsit5(), p = p) l = sum(abs, s_[end,end]) return l, s_ end loss(pnn) ps = typeof(solution)[] ls = eltype(p_init)[] callback = function (p, l, pred) display(l) push!(ps, pred) push!(ls, l) l <= 1.35 && return true return false end # Steer away from initial position and try to avoid local minima res_1 = DiffEqFlux.sciml_train(loss, pnn, cb = callback, maxiters = 100) anm = @animate for i in 1:1:length(ps) pl_ = plot(ps[i], ylim = (0, 4), title = "Iteration $i : $(ls[i])") plot!(ps[i].t, 1.34408f0*ones(length(ps[i].t)), color = :black, style = :dash, label = "Optimum") pl_ end gif(anm, joinpath(pwd(), "figures", "lotka_volterra_optimal_control.gif"), fps = 10) # Plot the control value s_ = solve(prob, Tsit5(), p = res_1.u, saveat = Δt) us = f(res_1.u)(permutedims(s_.t)) p1 = plot(s_, legend = :bottomright, ylabel = "u(t)") plot!(s_.t, 1.34408f0*ones(length(s_.t)), color = :black, style = :dash, label = "Optimum") plot( p1, plot(s_.t, us', xlabel = "t", ylabel = "w(t)", label = nothing, xticks = 0:2:12), layout = (2,1), link = :x ) savefig(joinpath(pwd(), "figures", "lotka_volterra_optimal_control_input.png")) plot(ls, title = "Objective", xlabel = "Iterations", label = nothing) savefig(joinpath(pwd(), "figures", "lotka_volterra_optimal_control_objective.png"))
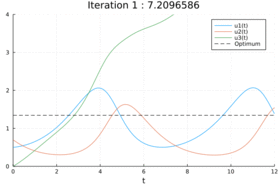
- Reference solution plot