Difference between revisions of "Gravity Turn Maneuver (Casadi)"
From mintOC
m |
(Corrected due to error in derivative of angle to vertical; added comments and intermediate expressions) |
||
| Line 10: | Line 10: | ||
from casadi import * | from casadi import * | ||
| − | N = 300 | + | # Artificial model parameters |
| − | vel_eps = 1e-6 | + | N = 300 # Number of shooting intervals |
| + | vel_eps = 1e-6 # Initial velocity (km/s) | ||
| − | m0 = 11.3 | + | # Vehicle parameters |
| − | m1 = 1.3 | + | m0 = 11.3 # Launch mass (t) |
| − | g0 = 9.81e-3 | + | m1 = 1.3 # Dry mass (t) |
| − | r0 = 6.0e2 | + | g0 = 9.81e-3 # Gravitational acceleration at altitude zero (km/s^2) |
| − | Isp = 300.0 | + | r0 = 6.0e2 # Radius at altitude zero (km) |
| − | Fmax = 600.0e-3 | + | Isp = 300.0 # Specific impulse (s) |
| + | Fmax = 600.0e-3 # Maximum thrust (MN) | ||
| − | cd = 0.021 | + | # Atmospheric parameters |
| − | A = 1.0 | + | cd = 0.021 # Drag coefficients |
| − | H = 5.6 | + | A = 1.0 # Reference area (m^2) |
| − | rho = (1.0 * 1.2230948554874) | + | H = 5.6 # Scale height (km) |
| + | rho = (1.0 * 1.2230948554874) # Density at altitude zero | ||
| − | h_obj = 75 | + | # Target orbit parameters |
| − | v_obj = 2.287 | + | h_obj = 75 # Target altitude (km) |
| − | q_obj = 0.5 * pi | + | v_obj = 2.287 # Target velocity (km/s) |
| + | q_obj = 0.5 * pi # Target angle to vertical (rad) | ||
| − | x = SX.sym('[m, v, q, h, d]') | + | # Create symbolic variables |
| − | u = SX.sym('u') | + | x = SX.sym('[m, v, q, h, d]') # Vehicle state |
| − | T = SX.sym('T') | + | u = SX.sym('u') # Vehicle controls |
| + | T = SX.sym('T') # Time horizon (s) | ||
| + | # Introduce symbolic expressions for important composite terms | ||
| + | Fthrust = Fmax * u | ||
| + | Fdrag = 0.5e3 * A * cd * rho * exp(-x[3] / H) * x[1]**2 | ||
| + | r = x[3] + r0 | ||
| + | g = g0 * (r0 / r)**2 | ||
| + | vhor = x[1] * sin(x[2]) | ||
| + | vver = x[1] * cos(x[2]) | ||
| + | |||
| + | # Build symbolic expressions for ODE right hand side | ||
| + | mdot = -(Fmax / (Isp * g0)) * u | ||
| + | vdot = (Fthrust - Fdrag) / x[0] - g * cos(x[2]) | ||
| + | hdot = vver | ||
| + | ddot = vhor / r | ||
| + | qdot = g * sin(x[2]) / x[1] - ddot | ||
| + | |||
| + | # Build the DAE function | ||
ode = [ | ode = [ | ||
| − | + | mdot, | |
| − | + | vdot, | |
| − | + | qdot, | |
| − | + | hdot, | |
| − | + | ddot | |
] | ] | ||
quad = u | quad = u | ||
| − | |||
dae = SXFunction("dae", daeIn(x=x, p=vertcat([u, T])), daeOut(ode=T*vertcat(ode), quad=T*quad)) | dae = SXFunction("dae", daeIn(x=x, p=vertcat([u, T])), daeOut(ode=T*vertcat(ode), quad=T*quad)) | ||
I = Integrator("I", "cvodes", dae, {'t0': 0.0, 'tf': 1.0 / N}) | I = Integrator("I", "cvodes", dae, {'t0': 0.0, 'tf': 1.0 / N}) | ||
| + | # Specify upper and lower bounds as well as initial values for DAE parameters, | ||
| + | # states and controls | ||
p_min = [120.0] | p_min = [120.0] | ||
p_max = [600.0] | p_max = [600.0] | ||
| Line 65: | Line 87: | ||
x_init = [0.5 * (m0 + m1), 0.5 * v_obj, 0.5 * q_obj, 0.5 * h_obj, 0.0] | x_init = [0.5 * (m0 + m1), 0.5 * v_obj, 0.5 * q_obj, 0.5 * h_obj, 0.0] | ||
| − | np = 1 | + | # Useful variable block sizes |
| − | nx = x.size1() | + | np = 1 # Number of parameters |
| − | nu = u.size1() | + | nx = x.size1() # Number of states |
| − | ns = nx + nu | + | nu = u.size1() # Number of controls |
| + | ns = nx + nu # Number of variables per shooting interval | ||
| + | # Introduce symbolic variables and disassemble them into blocks | ||
V = MX.sym('X', N * ns + nx + np) | V = MX.sym('X', N * ns + nx + np) | ||
P = V[0] | P = V[0] | ||
| Line 75: | Line 99: | ||
U = [V[np+i*ns+nx:np+(i+1)*ns] for i in range(0, N)] | U = [V[np+i*ns+nx:np+(i+1)*ns] for i in range(0, N)] | ||
| + | # Nonlinear constraints and Lagrange objective | ||
G = [] | G = [] | ||
F = 0.0 | F = 0.0 | ||
| + | # Build DMS structure | ||
x0 = p_init + x0_init | x0 = p_init + x0_init | ||
for i in range(0, N): | for i in range(0, N): | ||
| Line 87: | Line 113: | ||
x0 = x0 + u_init + [x0_init[i] + frac * (xf_init[i] - x0_init[i]) for i in range(0, nx)] | x0 = x0 + u_init + [x0_init[i] + frac * (xf_init[i] - x0_init[i]) for i in range(0, nx)] | ||
| + | # Lower and upper bounds for solver | ||
lbg = 0.0 | lbg = 0.0 | ||
ubg = 0.0 | ubg = 0.0 | ||
| Line 92: | Line 119: | ||
ubx = p_max + x0_max + u_max + (N-1) * (x_max + u_max) + xf_max | ubx = p_max + x0_max + u_max + (N-1) * (x_max + u_max) + xf_max | ||
| + | # Solve the problem using IPOPT | ||
nlp = MXFunction("nlp", nlpIn(x=V), nlpOut(f=m0 - X[-1][0], g=vertcat(G))) | nlp = MXFunction("nlp", nlpIn(x=V), nlpOut(f=m0 - X[-1][0], g=vertcat(G))) | ||
S = NlpSolver("S", "ipopt", nlp, {'tol': 1e-5}) | S = NlpSolver("S", "ipopt", nlp, {'tol': 1e-5}) | ||
| Line 101: | Line 129: | ||
'ubg': ubg | 'ubg': ubg | ||
}) | }) | ||
| − | |||
| − | == | + | # Extract state sequences and parameters from result |
| + | x = r['x'] | ||
| + | f = r['f'] | ||
| + | T = x[0] | ||
| − | + | t = [i * (T / N) for i in range(0, N+1)] | |
| + | m = x[np ::ns].get() | ||
| + | v = x[np+1::ns].get() | ||
| + | q = x[np+2::ns].get() | ||
| + | h = x[np+3::ns].get() | ||
| + | d = x[np+4::ns].get() | ||
| + | u = x[np+nx::ns].get() + [0.0] | ||
| + | </source> | ||
| − | + | == Results == | |
| − | + | ||
| − | + | The solution is calculated using IPOPT (3.11.9, default settings with tolerance 1e-5, using linear solver MUMPS in sequential mode on Ubuntu 15.10 for x86-64 with Linux 4.2.0-19-generic, Intel(R) Core(TM) i7-4790K CPU @ 4.00GHz, 16 GB RAM). The objective function value is <math>9.65080</math>. IPOPT finds the solution in 84 iterations (77.466 seconds proc time). | |
| − | + | ||
[[Category:CasADi]] | [[Category:CasADi]] | ||
Revision as of 15:09, 13 December 2015
This page contains a discretized version of the OCP Gravity Turn Maneuver in CasADi 2.4.2 format. The continuous model was discretized using a direct multiple shooting approach with 300 shooting nodes distributed equidistantly over a variable time horizon. The control grid is equal to the DMS grid. An initial solution is chosen by linearly interpolating between initial and terminal state.
CasADi
# ---------------------------------------------------------------- # Gravity Turn Maneuver with direct multiple shooting using CVodes # (c) Mirko Hahn # ---------------------------------------------------------------- from casadi import * # Artificial model parameters N = 300 # Number of shooting intervals vel_eps = 1e-6 # Initial velocity (km/s) # Vehicle parameters m0 = 11.3 # Launch mass (t) m1 = 1.3 # Dry mass (t) g0 = 9.81e-3 # Gravitational acceleration at altitude zero (km/s^2) r0 = 6.0e2 # Radius at altitude zero (km) Isp = 300.0 # Specific impulse (s) Fmax = 600.0e-3 # Maximum thrust (MN) # Atmospheric parameters cd = 0.021 # Drag coefficients A = 1.0 # Reference area (m^2) H = 5.6 # Scale height (km) rho = (1.0 * 1.2230948554874) # Density at altitude zero # Target orbit parameters h_obj = 75 # Target altitude (km) v_obj = 2.287 # Target velocity (km/s) q_obj = 0.5 * pi # Target angle to vertical (rad) # Create symbolic variables x = SX.sym('[m, v, q, h, d]') # Vehicle state u = SX.sym('u') # Vehicle controls T = SX.sym('T') # Time horizon (s) # Introduce symbolic expressions for important composite terms Fthrust = Fmax * u Fdrag = 0.5e3 * A * cd * rho * exp(-x[3] / H) * x[1]**2 r = x[3] + r0 g = g0 * (r0 / r)**2 vhor = x[1] * sin(x[2]) vver = x[1] * cos(x[2]) # Build symbolic expressions for ODE right hand side mdot = -(Fmax / (Isp * g0)) * u vdot = (Fthrust - Fdrag) / x[0] - g * cos(x[2]) hdot = vver ddot = vhor / r qdot = g * sin(x[2]) / x[1] - ddot # Build the DAE function ode = [ mdot, vdot, qdot, hdot, ddot ] quad = u dae = SXFunction("dae", daeIn(x=x, p=vertcat([u, T])), daeOut(ode=T*vertcat(ode), quad=T*quad)) I = Integrator("I", "cvodes", dae, {'t0': 0.0, 'tf': 1.0 / N}) # Specify upper and lower bounds as well as initial values for DAE parameters, # states and controls p_min = [120.0] p_max = [600.0] p_init = [120.0] u_min = [0.0] u_max = [1.0] u_init = [0.5] x0_min = [m0, vel_eps, 0.0, 0.0, 0.0] x0_max = [m0, vel_eps, 0.5 * pi, 0.0, 0.0] x0_init = [m0, vel_eps, 0.05 * pi, 0.0, 0.0] xf_min = [m1, v_obj, q_obj, h_obj, 0.0] xf_max = [m0, v_obj, q_obj, h_obj, inf] xf_init = [m1, v_obj, q_obj, h_obj, 0.0] x_min = [m1, vel_eps, 0.0, 0.0, 0.0] x_max = [m0, inf, pi, inf, inf] x_init = [0.5 * (m0 + m1), 0.5 * v_obj, 0.5 * q_obj, 0.5 * h_obj, 0.0] # Useful variable block sizes np = 1 # Number of parameters nx = x.size1() # Number of states nu = u.size1() # Number of controls ns = nx + nu # Number of variables per shooting interval # Introduce symbolic variables and disassemble them into blocks V = MX.sym('X', N * ns + nx + np) P = V[0] X = [V[np+i*ns:np+i*ns+nx] for i in range(0, N+1)] U = [V[np+i*ns+nx:np+(i+1)*ns] for i in range(0, N)] # Nonlinear constraints and Lagrange objective G = [] F = 0.0 # Build DMS structure x0 = p_init + x0_init for i in range(0, N): Y = I({'x0': X[i], 'p': vertcat([U[i], P])}) G = G + [Y['xf'] - X[i+1]] F = F + Y['qf'] frac = float(i+1) / N x0 = x0 + u_init + [x0_init[i] + frac * (xf_init[i] - x0_init[i]) for i in range(0, nx)] # Lower and upper bounds for solver lbg = 0.0 ubg = 0.0 lbx = p_min + x0_min + u_min + (N-1) * (x_min + u_min) + xf_min ubx = p_max + x0_max + u_max + (N-1) * (x_max + u_max) + xf_max # Solve the problem using IPOPT nlp = MXFunction("nlp", nlpIn(x=V), nlpOut(f=m0 - X[-1][0], g=vertcat(G))) S = NlpSolver("S", "ipopt", nlp, {'tol': 1e-5}) r = S({ 'x0' : x0, 'lbx': lbx, 'ubx': ubx, 'lbg': lbg, 'ubg': ubg }) # Extract state sequences and parameters from result x = r['x'] f = r['f'] T = x[0] t = [i * (T / N) for i in range(0, N+1)] m = x[np ::ns].get() v = x[np+1::ns].get() q = x[np+2::ns].get() h = x[np+3::ns].get() d = x[np+4::ns].get() u = x[np+nx::ns].get() + [0.0]
Results
The solution is calculated using IPOPT (3.11.9, default settings with tolerance 1e-5, using linear solver MUMPS in sequential mode on Ubuntu 15.10 for x86-64 with Linux 4.2.0-19-generic, Intel(R) Core(TM) i7-4790K CPU @ 4.00GHz, 16 GB RAM). The objective function value is 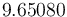 . IPOPT finds the solution in 84 iterations (77.466 seconds proc time).
. IPOPT finds the solution in 84 iterations (77.466 seconds proc time).