Gravity Turn Maneuver
| Gravity Turn Maneuver | |
|---|---|
| State dimension: | 1 |
| Differential states: | 5 |
| Continuous control functions: | 1 |
| Path constraints: | 11 |
| Interior point inequalities: | 2 |
| Interior point equalities: | 7 |
The gravity turn or zero lift turn is a common maneuver used to launch spacecraft into orbit from bodies that have non-negligible atmospheres. The goal of the maneuver is to minimize atmospheric drag by always orienting the vehicle along the velocity vector. In this maneuver, the vehicle's pitch is determined solely by the change of the velocity vector through gravitational acceleration and thrust. The goal is to find a launch configuration and thrust control strategy that achieves a specific orbit with minimal fuel consumption.
Contents
[hide]Physical description and model derivation
For the purposes of this model, we start with the following ODE system proposed by Culler et. al. in [Culler1957]The entry doesn't exist yet.:
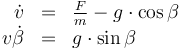
where 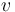 is the speed of the vehicle,
is the speed of the vehicle, 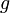 is the gravitational acceleration at the vehicle's current altitude,
is the gravitational acceleration at the vehicle's current altitude, 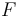 is the accelerating force and
is the accelerating force and 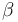 is the angle between the vertical and the vehicle's velocity vector. In the original version of the model, the authors neglect aspects of the problem:
is the angle between the vertical and the vehicle's velocity vector. In the original version of the model, the authors neglect aspects of the problem:
- Variation of
 over altitude
over altitude - Decrease of vehicle mass due to fuel consumption
- Curvature of the surface
- Atmospheric drag
Changes in gravitational acceleration
To account for changes in  , we make the following substitution:
, we make the following substitution:
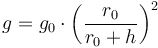
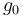 is the gravitational acceleration at altitude zero and
is the gravitational acceleration at altitude zero and 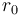 is the distance of altitude zero from the center of the reference body.
is the distance of altitude zero from the center of the reference body.
Decrease in vehicle mass
To account for changes in vehicle mass, we consider 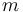 a differential state with the following derivative:
a differential state with the following derivative:
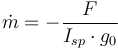
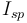 is the specific impulse of the vehicle's engine. Specific impulse is a measure of engine efficiency. For rocket engines, it directly correlates with the engine's exhaust velocity and may vary with atmospheric pressure, velocity, engine temperature and combustion dynamics. For the purposes of this model, we will assume it to be constant.
is the specific impulse of the vehicle's engine. Specific impulse is a measure of engine efficiency. For rocket engines, it directly correlates with the engine's exhaust velocity and may vary with atmospheric pressure, velocity, engine temperature and combustion dynamics. For the purposes of this model, we will assume it to be constant.
The vehicle's fuel reserve is modelled by two parameters: 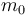 denotes the launch mass (with fuel) and
denotes the launch mass (with fuel) and 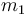 denotes the dry mass (without fuel).
denotes the dry mass (without fuel).
Curvature of the reference body's surface
To accomodate the reference body's curvature, we introduce an additional differential state 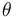 which represents the change in the vehicle's polar angle with respect to the launch site. The derivative is given by
which represents the change in the vehicle's polar angle with respect to the launch site. The derivative is given by
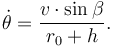
Note that the vertical changes as the vehicle moves around the reference body meaning that the derivative of 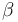 must be changed as well:
must be changed as well:
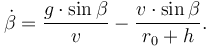
Atmospheric drag
To model atmospheric drag, we assume that the vehicles draf coefficient 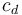 is constant. The drag force is given by
is constant. The drag force is given by
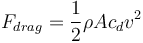
where 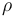 is the density of the atmosphere and
is the density of the atmosphere and 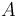 is the vehicle's reference area. We assume that atmospheric density decays exponentially with altitude:
is the vehicle's reference area. We assume that atmospheric density decays exponentially with altitude:
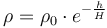
where 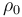 is the atmospheric density at altitude zero and
is the atmospheric density at altitude zero and 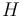 is the scale height of the atmosphere. The [drag force] is introduced into the acceleration term:
is the scale height of the atmosphere. The [drag force] is introduced into the acceleration term:
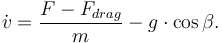
Note that if the vehicle is axially symmetric and oriented in such a way that its symmetry axis is parallel to the velocity vector, it does not experience any lift forces. This model is simplified. It does not account for changes in temperature and atmospheric composition with altitude. Also, 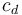 varies with fluid viscosity and vehicle velocity. Specifically, drastic changes in
varies with fluid viscosity and vehicle velocity. Specifically, drastic changes in 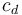 occur as the vehicle breaks the sound barrier. This is not accounted for in this model.
occur as the vehicle breaks the sound barrier. This is not accounted for in this model.
Mathematical formulation
The resulting optimal control problem is given by
![\begin{array}{llcll}
\displaystyle \min_{T, m, v, \beta, h, \theta, u} & m_0 - m(T) \\[1.5ex]
\mbox{s.t.} & \dot{m} & = & -\frac{F_{max}}{I_{sp} \cdot g_0} \cdot u ,\\
& \dot{v} & = & (F - \frac{1}{2} \rho_0 \cdot e^{-\frac{h}{H}} A c_d v^2) \cdot \frac{1}{m} - g_0 \cdot \left(\frac{r_0}{r_0 + h}\right)^2 \cos \beta ,\\
& \dot{\beta} & = & g_0 \cdot \left(\frac{r_0}{r_0 + h}\right)^2 \cdot \frac{\sin{\beta}}{v} - \frac{v \cdot \sin \beta}{r_0 + h} ,\\
& \dot{h} & = & v \cdot \cos \beta ,\\
& \dot{\theta} & = & \frac{v \cdot \sin \beta}{r_0 + h},\\[1.5ex]
& m(0) &=& m_0 , \\
& v(0) &=& \varepsilon , \\
& \beta(0) &\in& \left[ 0,\frac{\pi}{2} \right], \\
& h(0) &=& 0, \\
& \theta(0) &=& 0, \\[1.5ex]
& \beta(T) &=& \hat{\beta} , \\
& h(T) &=& \hat{h} , \\
& v(T) &=& \hat{v} , \\[1.5ex]
& m(t) &\in& [m_1, m_0] \qquad & \forall t \in [0,T] , \\
& v(t) &\geq& \varepsilon \qquad & \forall t \in [0,T] , \\
& \beta(t) &\in& [0, \pi] \qquad & \forall t \in [0,T] , \\
& h(t) &\geq& 0 \qquad & \forall t \in [0,T] , \\
& \theta(t) &\geq& 0 \qquad & \forall t \in [0,T] , \\[1.5ex]
& u(t) &\in& [0,1] \qquad & \forall t \in [0,T] , \\
& T &\in& [T_{min}, T_{max}].
\end{array}](https://mintoc.de/images/math/c/9/2/c924ca63bc1a55f04b24803be981651e.png)
where 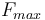 is the maximum thrust of the vehicle's engine and
is the maximum thrust of the vehicle's engine and 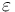 is a small number that is strictly greater than zero.
The differential states of the problem are
is a small number that is strictly greater than zero.
The differential states of the problem are 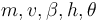 while
while 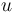 is the control function
is the control function
Parameters
For testing purposes, the following parameters were chosen:
![\begin{array}{rcl}
m_0 &=& 11.3 \; t \\
m_1 &=& 1.3 \; t \\
I_{sp} &=& 300 \; s \\
F_{max} &=& 0.6 \; MN \\
c_d &=& 0.021 \\
A &=& 1 \; m^2 \\[1.5ex]
g_0 &=& 9.81 \cdot 10^{-3} \, \frac{km}{s^2} \\
r_0 &=& 600.0 \; km \\
H &=& 5.6 \; km \\
\rho_0 &=& 1.2230948554874 \; \frac{kg}{m^3} \\[1.5ex]
\hat{\beta} &=& \; \frac{\pi}{2} \\
\hat{v} &=& 2.287 \; \frac{km}{s} \\
\hat{h} &=& 75 \; km \\[1.5ex]
T_{min} &=& 120 \; s \\
T_{max} &=& 600 \; s \\
\varepsilon &=& 10^{-6} \; \frac{km}{s}
\end{array}](https://mintoc.de/images/math/e/0/9/e09392aa4885a0177112eda1e80c2f5d.png)
Reference solution
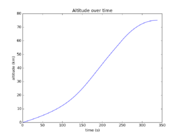
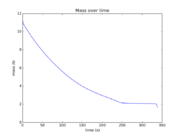
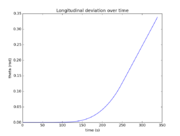
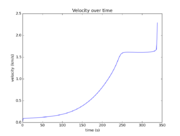
The reference solution was generated using a direct multiple shooting approach with 300 shooting intervals placed equidistantly along the variable-length time horizon. The resulting NLP was implemented using CasADi 2.4.2 using CVodes as an integrator and IPOPT as a solver. The exact code used to solve the problem alongside detailed solution data can be found under Gravity Turn Maneuver (Casadi). The solution achieves the desired orbit in 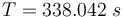 spending
spending 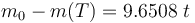 of fuel. The launch angle is approximately
of fuel. The launch angle is approximately 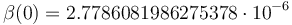 . The downrange motion throughout the entire launch amounts to a change in polar angle of approximately
. The downrange motion throughout the entire launch amounts to a change in polar angle of approximately 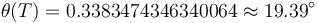 .
.
- Reference solution plots
Source Code
Model descriptions are available in
References
| [Culler1957] | The entry doesn't exist yet. |