Difference between revisions of "Bioreactor"

From mintOC
Jump to: navigation, search
m (SebastianSager moved page Bioreactor example to Bioreactor without leaving a redirect: example not needed)
Line 1: Line 1:
−
The bioreactor example is an easy bioreactor with an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in:
+
The bioreactor problem describes an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of the substrate. The problem is taken from the examples folder of the ACADO toolkit described in:
  
 
  Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
 
  Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."

Revision as of 09:19, 16 December 2015

The bioreactor problem describes an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of the substrate. The problem is taken from the examples folder of the ACADO toolkit described in: 

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Originally the problem seems to be motivated by: 

VERSYCK, KARINA J., and JAN F. VAN IMPE. "Feed rate optimization for fed-batch bioreactors: From optimal process performance to optimal parameter estimation."
Chemical Engineering Communications 172.1 (1999): 107-124.

Model Formulation

The dynamic model is an ODE model:

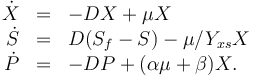
\begin{array}{rcl} \dot{X}&=&-DX+\mu X \\ \dot{S}&=& D(S_{f}-S)-\mu /Y_{xs} X \\ \dot{P}&=&-DP+ (\alpha \mu +\beta) X. \end{array}

The three states describe the concentration of the biomass (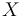X), the substrate (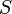S), and the product (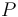P) in the reactor. In steady state the feed and outlet are equal and dilute all three concentrations with a ratio 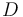D. The biomass grows with a rate 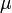\mu, while it eats up the substrate with the rate 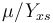\mu/Y_{xs} and produces product at a rate 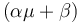(\alpha \mu +\beta). The rate 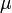\mu is given by:

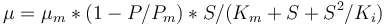
\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)

The fixed parameters (constants) of the model are as follows.

Parameters
Name Symbol Value Unit
Dilution 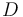D 0.15 [-]
Rate coefficient 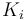K_i 22 [-]
Rate coefficient 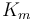K_m 1.2 [-]
Rate coefficient 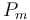P_m 50 [-]
Substrate to Biomass rate 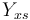Y_{xs} 0.4 [-]
Linear slope 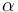\alpha 2.2 [-]
Linear intercept 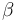\beta 0.2 [-]
Maximal growth rate 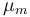\mu_m 0.48 [-]

Optimal Control Problem

Writing shortly for the states in vector notation 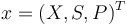x=(X,S,P)^T the OCP reads:

\begin{array}{cl} \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex] \mbox{s.t.} & \dot{x} = f(x,S_f), \forall \, t \in [0,48]\\ & x(0) = (6.5,12,22)^T \\ & x \in \R^3,\,S_f \in [28.7,40]. \end{array}

Objective

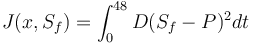
J(x,S_f)=\int_0^{48}D(S_f-P)^2dt

Reference Solution

Here we present the reference solution of the reimplemented example in the ACADO code generation with matlab. The source code is given in the next section.

  • Reference solution

  • Optimal solution for the ACADO example.

Source Code

This is the implementation of the ACADO bioreactor example with the matlab interface and the code generation of ACADO. 

% implements the bioreactor example of ACADO for the matlab interface and
% the code generation

clc;
clear all;
close all;

Ts = 0.1;
EXPORT = 1;

%% Variables
DifferentialState X S P;
Control Sf;

n_XD = length(diffStates);
n_U = length(controls);

%% Constants
D       = 0.15;
Ki      = 22.0;
Km      = 1.2 ; 
Pm      = 50.0;
Yxs     = 0.4 ;
alpha   = 2.2 ;
beta    = 0.2 ;
mum     = 0.48;
Sfmin   = 28.7;
Sfmax   = 40.0;
t_start =  0.0;
t_end   = 48.0;
N = 20;

%% Differential Equation
mu = mum*(1-P/Pm)*S/(Km+S+S^2/Ki);

f = dot([X;S;P]) == [-D*X+mu*X;...
                      D*(Sf-S)-(mu/Yxs)*X;...
		             -D*P+(alpha*mu+beta)*X];

% output
h = P-Sf;
hN = P;

%% MPCexport
acadoSet('problemname', 'mpc');

ocp = acado.OCP( t_start, t_end, N );

W_mat = D;
WN_mat = D;
W = acado.BMatrix(W_mat);
WN = acado.BMatrix(WN_mat);

ocp.minimizeLSQ( W, h );
ocp.minimizeLSQEndTerm( WN, hN );

ocp.subjectTo( Sfmin <= Sf <= Sfmax );
ocp.setModel(f);

mpc = acado.OCPexport( ocp );
mpc.set( 'HESSIAN_APPROXIMATION',       'GAUSS_NEWTON'      );
mpc.set( 'DISCRETIZATION_TYPE',         'MULTIPLE_SHOOTING' );
mpc.set( 'SPARSE_QP_SOLUTION',          'FULL_CONDENSING_N2');
mpc.set( 'INTEGRATOR_TYPE',             'INT_IRK_GL4'       );
mpc.set( 'NUM_INTEGRATOR_STEPS',        10*N                 );
mpc.set( 'QP_SOLVER',                   'QP_QPOASES'    	);
mpc.set( 'HOTSTART_QP',                 'NO'             	);
mpc.set( 'LEVENBERG_MARQUARDT', 		 1e-10				);

if EXPORT
    mpc.exportCode( 'export_MPC' );
    copyfile('../../../../../../external_packages/qpoases', 'export_MPC/qpoases')
    
    cd export_MPC
    make_acado_solver('../acado_MPCstep')
    cd ..
end

%% CONSTANTS FOR OPTIMIZATION
X0 = [6.5 12.0 22.0];
input.x0=X0';
Xref = [0 0 0];
input.x = repmat(Xref,N+1,1);
Xref = repmat(Xref,N,1);
input.od = [];

Uref = zeros(N,n_U);
input.u = Uref;

input.y = Sfmin*ones(N,1);
input.yN = Sfmin;

input.W = 1;
input.WN = 1;

%% SOLVER LOOP (SQP - Gauss newton)
display('------------------------------------------------------------------')
display('               SOLVER Loop'                                    )
display('------------------------------------------------------------------')



for i=1:20
    tic
    % Solve NMPC OCP
    output = acado_MPCstep(input);
    
    input.x=output.x;
    input.u=output.u;

    disp([' (RTI step: ' num2str(output.info.cpuTime*1e6) ' µs)'])

end

%% PLOT RESULTS

% States
figure(1)
plot([t_start:t_end/N:t_end],output.x)
ylabel('States')
xlabel('Time')
legend('X','S','P')

% Control
figure(2)
plot([t_start:t_end/N:t_end-t_end/N],output.u)
ylabel('Control (Sf)')
xlabel('Time')

% one figure for all
figure(3)
subplot(2,2,1)
plot([t_start:t_end/N:t_end],output.x(:,1))
ylabel('X')
xlabel('Time')
subplot(2,2,2)
plot([t_start:t_end/N:t_end],output.x(:,2))
ylabel('S')
xlabel('Time')
subplot(2,2,3)
plot([t_start:t_end/N:t_end],output.x(:,3))
ylabel('P')
xlabel('Time')
subplot(2,2,4)
plot([t_start:t_end/N:t_end-t_end/N],output.u)
ylabel('Sf')
xlabel('Time')
Retrieved from "https://mintoc.de/index.php?title=Bioreactor&oldid=1068"