Difference between revisions of "Catalyst mixing problem"
From mintOC
FelixMueller (Talk | contribs) |
FelixMueller (Talk | contribs) |
||
| Line 19: | Line 19: | ||
\begin{array}{llcl} | \begin{array}{llcl} | ||
\displaystyle \min_{x, u} &-1 + x_1(t_f) + x_2(t_f) \\[1.5ex] | \displaystyle \min_{x, u} &-1 + x_1(t_f) + x_2(t_f) \\[1.5ex] | ||
| − | \mbox{s.t.} & \dot{x}_1 & = & u ( 10 x_2 - x_1), \\ | + | \mbox{s.t.} |
| + | & \dot{x}_1 & = & u ( 10 x_2 - x_1), \\ | ||
& \dot{x}_2 & = & u ( x_1 - 10 x_2) - (1 - u \, x_2) , \\ | & \dot{x}_2 & = & u ( x_1 - 10 x_2) - (1 - u \, x_2) , \\ | ||
& x(t_0) &=& (1, 0)^T, \\ | & x(t_0) &=& (1, 0)^T, \\ | ||
Revision as of 19:03, 5 May 2016
| Catalyst mixing problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point equalities: | 2 |
The Catalyst mixing problem seeks an optimal policy for mixing two catalysts "along the length of a tubular plug ow reactor involving several reactions". (Cite and problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, u} &-1 + x_1(t_f) + x_2(t_f) \\[1.5ex]
\mbox{s.t.}
& \dot{x}_1 & = & u ( 10 x_2 - x_1), \\
& \dot{x}_2 & = & u ( x_1 - 10 x_2) - (1 - u \, x_2) , \\
& x(t_0) &=& (1, 0)^T, \\
& u(t) &\in& [0,1].
\end{array}](https://mintoc.de/images/math/6/d/7/6d73c1db6aa20b9386ac94b0e3142965.png)
Parameters
In this model the parameters used are 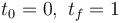 .
.
Source Code
Model descriptions are available in