Difference between revisions of "Fuller's initial value multimode problem"

From mintOC
Jump to: navigation, search
(Created page with "{{Dimensions |nd = 1 |nx = 2 |nw = 4 |nre = 2 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... --> This site descri...")
 
(→‎Reference Solutions)
Line 44: Line 44:
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of direct optimal control.  
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of direct optimal control.  
  
−
The optimal objective value of the relaxed problem with  <math> n_t=6000, \, n_u=100 </math> is <math>1.10988197e-05</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>3.94891656e-05</math>.   
+
The optimal objective value of the relaxed problem with  <math> n_t=6000, \, n_u=60 </math> is <math>1.08947605e-05</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>0.000422127329</math>.   
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="4">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="4">
−
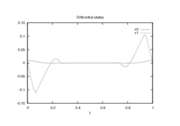
  Image:FullerRelaxed 6000 40 1.png| Optimal relaxed states determined by an direct approach with ampl_mintoc (Radau collocation)  and <math>n_t=6000, \, n_u=100</math>.
+
  Image:MmfullerRelaxed 6000 100 1.png| Optimal relaxed states determined by an direct approach with ampl_mintoc (Radau collocation)  and <math>n_t=6000, \, n_u=60</math>.
−
  Image:FullerRelaxed 6000 40 2.png| Optimal relaxed controls.
+
  Image:MmfullerRelaxed 6000 100 2.png| Optimal relaxed controls.
−
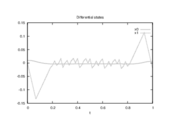
  Image:FullerCIA 6000 40 1.png| Optimal differential states trajectories of binary controls determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=6000, \, n_u=100</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
+
  Image:MmfullerCIA 6000 100 1.png| Optimal differential states trajectories of binary controls determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=6000, \, n_u=60</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
−
  Image:FullerCIA 6000 40 2.png| Optimal binary controls.
+
  Image:MmfullerCIA 6000 100 2.png| Optimal binary controls.
 
</gallery>
 
</gallery>
  

Revision as of 23:53, 8 January 2018

Fuller's initial value multimode problem
State dimension: 1
Differential states: 2
Discrete control functions: 4
Interior point equalities: 2
This site describes a Fuller's problem variant with no terminal constraints and additional Mayer term for penalizing deviation from given reference values. Furthermore, this variant comprises four binary controls instead of only one control.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w} & \int_{t_0}^{t_f} x_0^2 & \; \mathrm{d} t & + (x(t_f)-x_T)^2 \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & x_1+ \sum\limits_{i=1}^{4} c_{0,i} \omega_i, \\ & \dot{x}_1 & = & 1 + \sum\limits_{i=1}^{4} c_{1,i} \omega_i, \\[1.5ex] & 1 &=& \sum\limits_{i=1}^{4}w_i(t), \\ & x(0) &=& x_S, \\ & w(t) &\in& \{0, 1\}. \end{array}

Parameters

We use 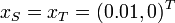x_S = x_T = (0.01, 0)^T together with:

\begin{array}{rcl} [t_0, t_f] &=& [0, 1],\\ (c_{0,1}, c_{1,1}) &=& (0, -2),\\ (c_{0,2}, c_{1,2}) &=& (0, -0.5),\\ (c_{0,3}, c_{1,3}) &=& (0, -3),\\ (c_{0,4}, c_{1,4}) &=& (0, 0). \end{array}


Reference Solutions

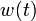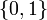If the problem is relaxed, i.e., we demand that w(t) be in the continuous interval [0, 1] instead of the binary choice \{0,1\}, the optimal solution can be determined by means of direct optimal control.

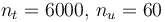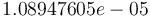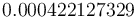The optimal objective value of the relaxed problem with n_t=6000, \, n_u=60 is 1.08947605e-05. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 0.000422127329.

  • Reference solution plots

  • Optimal relaxed states determined by an direct approach with ampl_mintoc (Radau collocation) and n_t=6000, \, n_u=60.

  • Optimal relaxed controls.

  • Optimal differential states trajectories of binary controls determined by an direct approach (Radau collocation) with ampl_mintoc and n_t=6000, \, n_u=60. The relaxed controls were approximated by Combinatorial Integral Approximation.

  • Optimal binary controls.

Retrieved from "https://mintoc.de/index.php?title=Fuller%27s_initial_value_multimode_problem&oldid=2189"