Difference between revisions of "Supermarket refrigeration system"

From mintOC
Jump to: navigation, search
(first ugly version)
 
(Added interpolation polynomials)
Line 23: Line 23:
 
\begin{array}{llcl}
 
\begin{array}{llcl}
 
  \displaystyle \min_{x,u} & \frac {1}{t_f - t_0}\int_{t_0}^{t_f}\dot{V}_{comp} \cdot f dt \\[1.5ex]
 
  \displaystyle \min_{x,u} & \frac {1}{t_f - t_0}\int_{t_0}^{t_f}\dot{V}_{comp} \cdot f dt \\[1.5ex]
−
  \mbox{s.t.} & \dot{x_0}(t) &=&  \dfrac{1}{V\_SUC \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[  
+
  \mbox{s.t.} & \dot{x_0}(t) &=&  \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[  
−
                     \left(\dfrac{UA_{wall-ref, max}}{M\_REF\_MAX \cdot
+
                     \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot
 
                     \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\  
 
                     \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\  
−
&          &&  + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M\_REF\_CONST \\
+
&          &&  + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const} \\
 
&          &&  - ETA\_VOL
 
&          &&  - ETA\_VOL
 
                     \cdot V\_SL \cdot 0.01 \, \left(u_2+u_3\right) \rho_{suc}(x_0)  
 
                     \cdot V\_SL \cdot 0.01 \, \left(u_2+u_3\right) \rho_{suc}(x_0)  
Line 84: Line 84:
 
</math>
 
</math>
  
−
+
The following polynomial functions are used in the model description and originate from interpolations:
 +
 
 +
<math>
 +
\begin{array}{rcl}
 +
 
 +
T_e(x_0)                            &=& -4.3544 x_0^2 + 29.224 x_0 - 51.2005,\\
 +
\Delta h_{lg}(x_0)                  &=& (0.0217 x_0^2 - 0.1704 x_0 + 2.2988)\cdot 10^5, \\
 +
\rho_{suc}(x_0)                      &=& 4.6073 x_0 + 0.3798, \\
 +
\frac{d\rho_{suc}}{dP_{suc}}(x_0)    &=& -0.0329 \cdot {x_0}^3 + 0.2161 \cdot {x_0}^2 - 0.4742 \cdot x_0 + 5.4817,\\
 +
f(x_0)                              &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5.
 +
 
 +
 
 +
 
 +
\end{array}
 +
</math>
 +
 
 
Here the differential state <math>x_0</math> describes the suction pressure in the suction manifold (in bar). The next three states model temperatures in the first display case (in °C). <math>x_1</math> is the goods' temperature, <math>x_2</math> the one of the evaporator wall and <math>x_3</math> the air temperature surrounding the goods. <math>x_4</math> then models the mass of the liquefied refrigerant in the evaporator (in kg).
 
Here the differential state <math>x_0</math> describes the suction pressure in the suction manifold (in bar). The next three states model temperatures in the first display case (in °C). <math>x_1</math> is the goods' temperature, <math>x_2</math> the one of the evaporator wall and <math>x_3</math> the air temperature surrounding the goods. <math>x_4</math> then models the mass of the liquefied refrigerant in the evaporator (in kg).
  
Line 229: Line 244:
  
 
* No periodicity was required but the solution on a fixed time horizon 4 hours - 2 in day scenario and 2 in night scenario - with <math>t_f = 14400</math> was asked.
 
* No periodicity was required but the solution on a fixed time horizon 4 hours - 2 in day scenario and 2 in night scenario - with <math>t_f = 14400</math> was asked.
 +
* The number of compressors and display cases is not fixed. Larsen also proposed the problem with 3 compressors and 3 display cases. This leads to a change in the compressor rack's preformance to <math>V_{sl} = 0.095 \frac{m^3}{s}</math>. Unfortunately this constant is only given for these two cases although Larsen proposed scenarios with more compressors and display cases.
  
 
== References ==
 
== References ==

Revision as of 12:29, 13 November 2008

Supermarket refrigeration system
State dimension: 1
Differential states: 9
Discrete control functions: 4
Interior point inequalities: 5


The supermarket refrigeration system problem is based on a model describing a refrigeration system with 2 parallel connected compressors which only can be controlled stepwise (each single compressor can be turned on or off) and 2 display cases containing goods needed to be refrigerated. Each display case is connected to the refrigeration circuit through an expansion valve which also can only be closed or opened.

The air temperatures surrounding the goods in each display case are modeled by one differential state each. These states have to be bounded, so that the goods are properly refrigerated.

The model was published by Larsen et. al. in 2007 <bibref>Larsen2007</bibref>. The main goal is to control the refirgeration system energy-optimal. The problem was set up as a benchmark problem for MIOCPs.

The mathematical equations form an ODE Model. The initial values of the differential states are not fixed but periodicity of the whole process is required.

The optimal integer control functions shows chattering behavior, making the supermarket refrigeration system problem a candidate for benchmarking of algorithms.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x,u} & \frac {1}{t_f - t_0}\int_{t_0}^{t_f}\dot{V}_{comp} \cdot f dt \\[1.5ex] \mbox{s.t.} & \dot{x_0}(t) &=& \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[ \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\ & && + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const} \\ & && - ETA\_VOL \cdot V\_SL \cdot 0.01 \, \left(u_2+u_3\right) \rho_{suc}(x_0) \bigg] \\ &\dot{x_1}(t) &=& - \dfrac{ UA\_GOODS\_AIR \left( x_1 - x_3 \right) }{ M\_GOODS \cdot C\_P\_GOODS } \\ \\ &\dot{x_2}(t) &=& \dfrac{ UA\_AIR\_WALL \left( x_3-x_2 \right) - \dfrac{UA\_WALL\_REF\_MAX}{M\_REF\_MAX} \, x_4 \big( x_2 - T_e(x_0) \big) }{ M\_WALL \cdot C\_P\_WALL } \\ \\ \\[1.5ex] &\dot{x_3}(t) &=& \dfrac{ UA\_GOODS\_AIR \left( x_1-x_3 \right) + Q\_AIRLOAD - UA\_AIR\_WALL \, (x_3-x_2) }{ M\_AIR \cdot C\_P\_AIR } \\ \\ &\dot{x_4}(t) &=& \dfrac{M\_REF\_MAX - x_4}{TAU\_FILL} u_0 - \dfrac{UA\_WALL\_REF\_MAX}{M\_REF\_MAX \cdot \Delta h_{lg}(x_0)} \, x_4 \big( x_2 - T_e(x_0) \big) (1-u_0) \\ \\ &\dot{x_5}(t) &=& - \dfrac{ UA\_GOODS\_AIR \left( x_5 - x_7 \right) }{ M\_GOODS \cdot C\_P\_GOODS } \\ \\ &\dot{x_6}(t) &=& \dfrac{ UA\_AIR\_WALL \left( x_7-x_6 \right) - \dfrac{UA\_WALL\_REF\_MAX}{M\_REF\_MAX} \, x_8 \big( x_6 - T_e(x_0) \big) }{ M\_WALL \cdot C\_P\_WALL } \\ \\ \\[1.5ex] &\dot{x_7}(t) &=& \dfrac{ UA\_GOODS\_AIR \left( x_5-x_7 \right) + Q\_AIRLOAD - UA\_AIR\_WALL \, (x_7-x_6) }{ M\_AIR \cdot C\_P\_AIR } \\ \\ &\dot{x_8}(t) &=& \dfrac{M\_REF\_MAX - x_4}{TAU\_FILL} u_0 - \dfrac{UA\_WALL\_REF\_MAX}{M\_REF\_MAX \cdot \Delta h_{lg}(x_0)} \, x_8 \big( x_6 - T_e(x_0) \big) (1-u_0) \\ \\ & 2.0 &\leq& x_3(t), x_7(t) \leq 5.0 \quad \forall t \in [t_0, t_f],\\ & x_0(t) &\leq& 1.7 \quad \forall t \in [t_0, t_f], \\ & x_i(t_0) &=& free \quad \forall i \in \{1,\dots 9\}, \\ & x_i(t_f) &=& x(t_0) \quad \forall i \in \{1,\dots 9\}, \\ & u_i(t) &\in& \{0, 1\} \quad \forall i \in \{1,\dots 4\}, \\ & t_f &\in& [ 650, 750 ]. \\ \end{array}

The following polynomial functions are used in the model description and originate from interpolations:

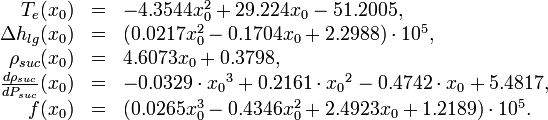
\begin{array}{rcl} T_e(x_0) &=& -4.3544 x_0^2 + 29.224 x_0 - 51.2005,\\ \Delta h_{lg}(x_0) &=& (0.0217 x_0^2 - 0.1704 x_0 + 2.2988)\cdot 10^5, \\ \rho_{suc}(x_0) &=& 4.6073 x_0 + 0.3798, \\ \frac{d\rho_{suc}}{dP_{suc}}(x_0) &=& -0.0329 \cdot {x_0}^3 + 0.2161 \cdot {x_0}^2 - 0.4742 \cdot x_0 + 5.4817,\\ f(x_0) &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5. \end{array}

Here the differential state 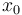x_0 describes the suction pressure in the suction manifold (in bar). The next three states model temperatures in the first display case (in °C). 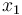x_1 is the goods' temperature, 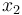x_2 the one of the evaporator wall and 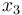x_3 the air temperature surrounding the goods. 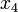x_4 then models the mass of the liquefied refrigerant in the evaporator (in kg).

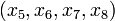(x_5, x_6, x_7, x_8) describe the corresponding states in the second display case.

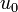u_0 describes the inlet valve of the first display case, 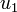u_1 respectively the valve of the second display case. 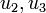u_2, u_3 denote the activity of a single compressor.

Parameters

These fixed values are used within the model. TODO: night scenario

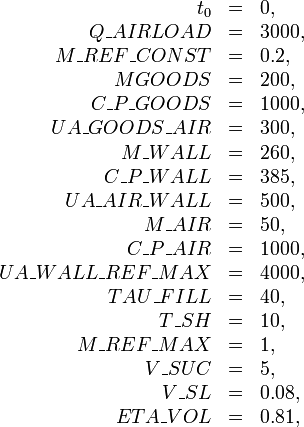
\begin{array}{rcl} t_0 &=& 0,\\ Q\_AIRLOAD &=& 3000, \\ M\_REF\_CONST &=& 0.2, \\ MGOODS &=& 200, \\ C\_P\_GOODS &=& 1000, \\ UA\_GOODS\_AIR &=& 300, \\ M\_WALL &=& 260, \\ C\_P\_WALL &=& 385, \\ UA\_AIR\_WALL &=& 500, \\ M\_AIR &=& 50, \\ C\_P\_AIR &=& 1000, \\ UA\_WALL\_REF\_MAX &=& 4000, \\ TAU\_FILL &=& 40, \\ T\_SH &=& 10, \\ M\_REF\_MAX &=& 1, \\ V\_SUC &=& 5, \\ V\_SL &=& 0.08, \\ ETA\_VOL &=& 0.81, \\ \end{array}

Reference Solutions

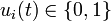For the relaxed problem (we only demand u_i(t) \in [0,1] instead of u_i(t) \in \{0,1\} the optimal solution is 12072.45. If we restrict ourselves to a solution with only integer controls we obtain the optimum objective value 12252.81.

Source Code

C

The differential equations in C code: 

// number of compressors
#define NVALVES 2
 
// constants
#define M_GOODS 200.0
#define C_P_GOODS 1000.0
#define UA_GOODS_AIR 300.0
#define M_WALL 260.0
#define C_P_WALL 385.0
#define UA_AIR_WALL 500.0
#define M_AIR 50.0
#define C_P_AIR 1000.0
#define UA_WALL_REF_MAX 4000.0
#define M_REF_MAX 1.0
#define TAU_FILL 40.0
#define T_SH 10.0
#define V_SUC 5.0
#define V_SL 0.08 // 2 display cases - 2 compressors
// #define V_SL 0.095 // 3 display cases - 3 compressors
#define ETA_VOL 0.81
 
// disturbances - day scenario
#define Q_AIRLOAD 3000.0
#define M_REF_CONST 0.2
 
// disturbances - night scenario
// #define Q_AIRLOAD 1800.0
// #define M_REF_CONST 0.0
 
double delta_h = (0.0217*xd[0]*xd[0] - 0.1704*xd[0] + 2.2988)*1e5;
double T_e = -4.3544*xd[0]*xd[0] + 29.224*xd[0] - 51.2005;
double rho_suc = 4.6073*xd[0] + 0.3798;
double rho_suc__P_suc = -0.0329*xd[0]*xd[0]*xd[0] + 0.2161*xd[0]*xd[0] - 0.4742*xd[0] + 5.4817;
double f = (0.0265*xd[0]*xd[0]*xd[0] -0.4346*xd[0]*xd[0] + 2.4923*xd[0] + 1.2189)*1e5;
 
double Q_goods_air[NVALVES];
double Q_air_wall[NVALVES];
double UA_wall_ref[NVALVES];
double Q_e[NVALVES];
double m[NVALVES];
 
double m_in_suc = 0.0;
 
int i;
    for (i=0; i<NVALVES; i++){
        Q_goods_air[i] = UA_GOODS_AIR*(xd[1 + i*4] - xd[3 + i*4]);
        Q_air_wall[i] = UA_AIR_WALL*(xd[3 + i*4] - xd[2 + i*4]);
        UA_wall_ref[i] = UA_WALL_REF_MAX * xd[4 + 4*i]/M_REF_MAX;
        Q_e[i] = UA_wall_ref[i]*(xd[2 + 4*i] - T_e);
 
        m[i] = Q_e[i]/delta_h;
        m_in_suc += m[i];
}
 
    double V_comp = 0.0;
    double comp_scale = (double) 1.0/NCOMPS;
    V_comp = comp_scale*u[NVALVES]*ETA_VOL*V_SL;
 
 
 
    // suction pressure
	rhs[0] = (m_in_suc + M_REF_CONST - V_comp*rho_suc) / (V_SUC*rho_suc__P_suc);
 
    // for each display/valve
    for (i=0; i<NVALVES; i++){
        // temperatures:
        // goods
        rhs[1 + i*4] = - Q_goods_air[i]/(M_GOODS*C_P_GOODS);
        // wall
        rhs[2 + i*4] = (Q_air_wall[i] - Q_e[i])/(M_WALL*C_P_WALL);
        // air
        rhs[3 + i*4] = ((Q_goods_air[i] + Q_AIRLOAD - Q_air_wall[i])
		        /(M_AIR*C_P_AIR));
 
        // mass of liquefied refrigerant:
        rhs[4 + i*4] = ((M_REF_MAX - xd[4 + 4*i])/TAU_FILL * u[i]
		        - m[i] * (1 - u[i]));
}


Variants

There are several alternative formulations and variants of the above problem, in particular

In the paper <bibref>Larsen2007</bibref> mentioned above, the problem was stated slightly different:

  • The temperature constraints weren't hard bounds but there was a penalization term added to the objective function to minimize the violation of these constraints.
  • A night scenario with two different parameters was given. At night the following parameters change their value:

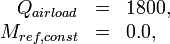
\begin{array}{rcl} Q_{airload} &=& 1800, \\ M_{ref,const} &=& 0.0, \\ \end{array}

  • No periodicity was required but the solution on a fixed time horizon 4 hours - 2 in day scenario and 2 in night scenario - with 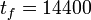t_f = 14400 was asked.
  • The number of compressors and display cases is not fixed. Larsen also proposed the problem with 3 compressors and 3 display cases. This leads to a change in the compressor rack's preformance to 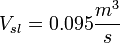V_{sl} = 0.095 \frac{m^3}{s}. Unfortunately this constant is only given for these two cases although Larsen proposed scenarios with more compressors and display cases.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=Supermarket_refrigeration_system&oldid=278"