Supermarket refrigeration system

From Mintoc

Jump to: navigation, search
The supermarket refrigeration system problem is based on a model describing a refrigeration system with 2 parallel connected compressors (called a compressor rack) which only can be controlled stepwise (each single compressor can be turned on or off) and 2 open refrigerated display cases containing goods needed to be refrigerated. Each display case is connected to the refrigeration circuit through an expansion valve which also can only be closed or opened. This valve controls the flow of refrigerant into the evaporator, where it absorbs heat from the surrounding air. The refrigerated air then creates the well-known air-curtain at the front of the display case. The air temperatures surrounding the goods in each display case are modeled by one differential state each. These states have to be bounded, so that the goods are properly refrigerated. The model was published by Larsen et. al. in 2007 [1]. The main goal is to control the refirgeration system energy-optimal. The problem was set up as a benchmark problem for MIOCPs. The mathematical equations form an ODE model. The initial values of the differential states are not fixed but periodicity of the whole process is required. The optimal integer control function shows chattering behavior, making the supermarket refrigeration system problem a candidate for benchmarking of algorithms.
Supermarket refrigeration system
State dimension: 1
Differential states: 9
Discrete control functions: 3
Interior point equalities: 9

Contents

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

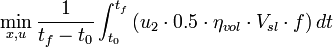
\min_{x,u} \frac {1}{t_f - t_0}\int_{t_0}^{t_f} \left( u_2 \cdot 0.5 \cdot \eta_{vol} \cdot V_{sl} \cdot f \right) dt

\begin{array}{llcl} \displaystyle \mbox{s.t.} & \dot{x_0}(t) &=& \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[ \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\ & && + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const} - \eta_{vol} \cdot V_{sl} \cdot 0.5 \, u_2 \rho_{suc}(x_0) \bigg] \\ &\dot{x_1}(t) &=& - \dfrac{ UA_{goods-air} \left( x_1 - x_3 \right) }{ M_{goods} \cdot C_{p,goods} } \\ &\dot{x_2}(t) &=& \dfrac{ UA_{air-wall} \left( x_3-x_2 \right) - \dfrac{UA_{wall-ref,max}}{M_{ref,max}} \, x_4 \big( x_2 - T_e(x_0) \big) }{ M_{wall} \cdot C_{p,wall} } \\ [2.5ex] &\dot{x_3}(t) &=& \dfrac{ UA_{goods-air} \left( x_1-x_3 \right) + \dot{Q}_{airload} - UA_{air-wall} \, (x_3-x_2) }{ M_{air} \cdot C_{p,air} } \\ [2.5ex] &\dot{x_4}(t) &=& \left(\dfrac{M_{ref,max} - x_4}{\tau_{fill}} \right) u_0 - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \, x_4 \big( x_2 - T_e(x_0) \big) \right) (1-u_0) \\ \\ &\dot{x_5}(t) &=& - \dfrac{ UA_{goods-air} \left( x_5 - x_7 \right) }{ M_{goods} \cdot C_{p,goods} } \\ &\dot{x_6}(t) &=& \dfrac{ UA_{air-wall} \left( x_7-x_6 \right) - \dfrac{UA_{wall-ref,max}}{M_{ref,max}} \, x_8 \big( x_6 - T_e(x_0) \big) }{ M_{wall} \cdot C_{p,wall} } \\ [2.5ex] &\dot{x_7}(t) &=& \dfrac{ UA_{goods-air} \left( x_5-x_7 \right) + \dot{Q}_{airload} - UA_{air-wall} \, (x_7-x_6) }{ M_{air} \cdot C_{p,air} } \\ [2.5ex] &\dot{x_8}(t) &=& \left(\dfrac{M_{ref,max} - x_8}{\tau_{fill}} \right) u_1 - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \, x_8 \big( x_6 - T_e(x_0) \big) \right) (1-u_1) \\ [4ex] & x_3(t) &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\ & x_3(t) &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\ & x_7(t) &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\ & x_7(t) &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\ & x_0(t) &\leq& 1.7 \quad \forall t \in [t_0, t_f], \\ & x_i(t_0) &=& free \quad \forall i \in \{0,\dots, 8\}, \\ & x_i(t_f) &=& x_i(t_0) \quad \forall i \in \{0,\dots, 8\}, \\ & u_i(t) &\in& \{0, 1\} \quad \forall i \in \{0,\dots, 2\}, \\ & t_f &\in& [ 650, 750 ]. \end{array}


Here the differential state 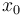x0 describes the suction pressure in the suction manifold (in bar). The next three states model temperatures in the first display case (in °C). 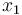x1 is the goods' temperature, 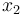x2 the one of the evaporator wall and 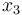x3 the air temperature surrounding the goods. 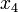x4 then models the mass of the liquefied refrigerant in the evaporator (in kg).

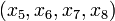(x5,x6,x7,x8) describe the corresponding states in the second display case.

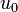u0 describes the inlet valve of the first display case, 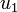u1 respectively the valve of the second display case. 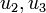u2,u3 denote the activity of a single compressor.

The following polynomial functions are used in the model description originating from interpolations:

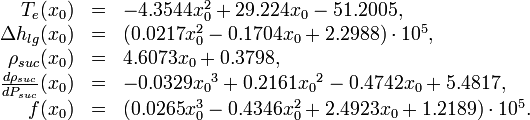
\begin{array}{rcl} T_e(x_0) &=& -4.3544 x_0^2 + 29.224 x_0 - 51.2005,\\ \Delta h_{lg}(x_0) &=& (0.0217 x_0^2 - 0.1704 x_0 + 2.2988)\cdot 10^5, \\ \rho_{suc}(x_0) &=& 4.6073 x_0 + 0.3798, \\ \frac{d\rho_{suc}}{dP_{suc}}(x_0) &=& -0.0329 {x_0}^3 + 0.2161 {x_0}^2 - 0.4742 x_0 + 5.4817,\\ f(x_0) &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5. \end{array}

Parameters

These fixed values are used within the model for the day scenario. A night scenario is also available, see Variants.

Symbol Value Unit Description
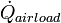\dot{Q}_{airload} 3000.00 \frac{J}{s} Disturbance, heat transfer from outside the display case
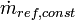\dot{m}_{ref,const} 0.20 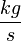\frac{kg}{s} Disturbance, constant mass flow of refrigerant

from unmodeled entities

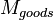Mgoods 200.00 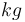kg Mass of goods
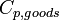Cp,goods 1000.00 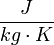\frac{J}{kg \cdot K} Heat capacity of goods
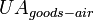UAgoods − air 300.00 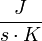\frac{J}{s \cdot K} Heat transfer coefficient between goods

and air

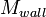Mwall 260.00 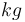kg Mass of evaporator wall
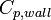Cp,wall 385.00 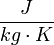\frac{J}{kg \cdot K} Heat capacity of evaporator wall
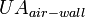UAair − wall 500.00 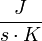\frac{J}{s \cdot K} Heat transfer coefficient between air and

wall

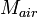Mair 50.00 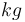kg Mass of air in display case
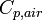Cp,air 1000.00 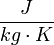\frac{J}{kg \cdot K} Heat capacity of air
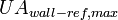UAwall − ref,max 4000.00 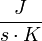\frac{J}{s \cdot K} Maximum heat transfer coefficient between

refrigerant and evaporator wall

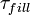τfill 40.00 s Parameter describing the filling time of the

evaporator under opened valve

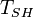TSH 10.00 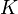K Superheat in the suction manifold
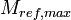Mref,max 1.00 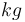kg Maximum mass of refrigerant in evaporator
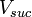Vsuc 5.00 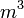m3 Total volume of suction manifold
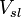Vsl 0.08 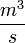\frac{m^3}{s} Total displacement volume
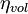ηvol 0.81 − Volumetric efficiency

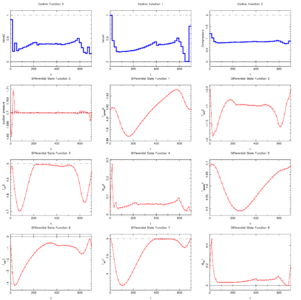
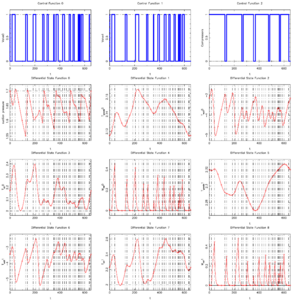
Reference Solutions

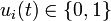For the relaxed problem (we only demand u_i(t) \in [0,1] instead of u_i(t) \in \{0,1\} the optimal solution is 12072.45. The illustrated solution with integer controls has a (suboptimal) objective function value of 12252.81.

Reference solution plots

Optimal relaxed control.

Optimal integer control.

Source Code

Model descriptions are available in

Variants

Since the compressors are parallel connected one can introduce a single control 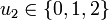u_2 \in \{0,1,2\} instead of two equivalent controls. The same holds for scenarions with 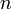n parallel connected compressors.

In the paper [1] mentioned above, the problem was stated slightly different:

  • The temperature constraints weren't hard bounds but there was a penalization term added to the objective function to minimize the violation of these constraints.
  • The differential equation for the mass of the refrigerant had another switch, if the valve (e.g. u0) is closed. It was formulated this way:

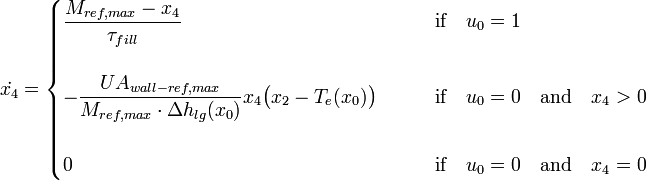
\dot{x_4} = \begin{cases} \dfrac{M_{ref,max} - x_4}{\tau_{fill}} & \qquad \text{if} \quad u_0 = 1 \\ \\ - \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} x_4 \big( x_2 - T_e(x_0) \big) & \qquad \text{if} \quad u_0 = 0 \quad \text{and}\quad x_4 > 0 \\ \\ 0 & \qquad \text{if} \quad u_0 = 0 \quad \text{and} \quad x_4 = 0 \end{cases}

This additional switch is redundant because the mass itself is a factor on the right hand side and so the complete right hand side is 0 if 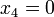x4 = 0.

  • A night scenario with two different parameters was given. At night the following parameters change their value:

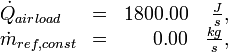
\begin{array}{lcrr} \dot{Q}_{airload} &=& 1800.00 & \frac{J}{s}, \\ \dot{m}_{ref,const} &=& 0.00 & \frac{kg}{s}, \\ \end{array}

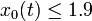Additionally the constraint on the suction pressure x0(t) is softened to x_0(t) \leq 1.9.

  • No periodicity was required but the solution on a fixed time horizon 4 hours - 2 in day scenario and 2 in night scenario - with 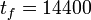tf = 14400 was asked.
  • The number of compressors and display cases is not fixed. Larsen also proposed the problem with 3 compressors and 3 display cases. This leads to a change in the compressor rack's preformance to 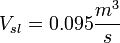V_{sl} = 0.095 \frac{m^3}{s}. Unfortunately this constant is only given for these two cases although Larsen proposed scenarios with more compressors and display cases.

References

  1. ↑ 1.0 1.1 Larsen, L. F. S., Izadi-Zamanabadi, R., Wisniewski, R., & Sonntag, C. (2007). Supermarket Refrigeration Systems – A benchmark for the optimal control of hybrid systems Technical report for the HYCON NoE. Bib
Retrieved from "http://www.mintoc.de/index.php/Supermarket_refrigeration_system"
Personal tools