Difference between revisions of "F-8 aircraft"

F-8 aircraft
State dimension:	1
Differential states:	3
Discrete control functions:	1
Interior point equalities:	6

Revision as of 15:52, 8 April 2009

The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by Kaya and Noakes and aims at controlling an aircraft in a time-optimal way from an initial state to a terminal state.

The mathematical equations form a small-scale ODE model. The interior point equality conditions fix both initial and terminal values of the differential states.

The optimal integer control functions shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.

Mathematical formulation

For $t \in [0, T]$ almost everywhere the mixed-integer optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& - 20.967 \; w + 6.265 \; x_0^2 \; w + 46 \; x_0 \; w^2 + 61.4 \; w^3 \\ & x(0) &=& (0.4655,0,0)^T, \\ & x(T) &=& (0,0,0)^T, \\ & w(t) &\in& \{-0.05236,0.05236\}. \end{array}$

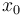$x_0$ is the angle of attack in radians, 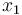$x_1$ is the pitch angle, 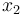$x_2$ is the pitch rate in rad/s, and the control function 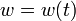$w = w(t)$ is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>.

In the control problem, both initial and terminal values of the differential states are fixed.

Reformulation

The control w(t) is restricted to take values from a finite set only. Hence, the control problem can be reformulated equivalently to

$\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& - \left( 0.215 \; \xi - 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 - 0.63 \; \xi^3 \right) \; w \\ &&& - \left( - 0.215 \; \xi + 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 + 0.63 \; \xi^3 \right) \; (1 - w) \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& - \left( 20.967 \; \xi - 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 - 61.4 \; \xi^3 \right) \; w \\ &&& - \left( - 20.967 \; \xi + 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 + 61.4 \; \xi^3 \right) \; (1 - w) \\ & x(0) &=& (0.4655,0,0)^T, \\ & x(T) &=& (0,0,0)^T, \\ & w(t) &\in& \{0,1\}, \end{array}$

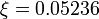with $\xi = 0.05236$ . Note that there is a bijection between optimal solutions of the two problems.

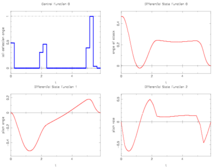
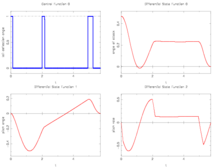
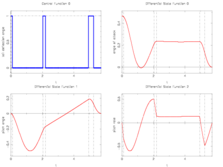
Reference solutions

We provide here a comparison of different solutions reported in the literature. The numbers show the respective lengths 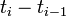$t_i - t_{i-1}$ of the switching arcs with the value of 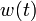$w(t)$ on the upper or lower bound (given in the second column). Claim denotes what is stated in the respective publication, Simulation shows values obtained by a simulation with a Runge-Kutta-Fehlberg method of 4th/5th order and an integration tolerance of $10^{-8}$ .

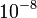Arc	w(t)	Lee et al.<bibref>Lee1997a</bibref>	Kaya<bibref>Kaya2003</bibref>	Sager<bibref>Sager2005</bibref>
1	1	0.00000	0.10292	0.10235
2	0	2.18800	1.92793	1.92812
3	1	0.16400	0.16687	0.16645
4	0	2.88100	2.74338	2.73071
5	1	0.33000	0.32992	0.32994
6	0	0.47200	0.47116	0.47107
Claim: Infeasibility	-	1.00E-10	7.30E-06	5.90E-06
Claim: Objective	-	6.03500	5.74217	5.72864
Simulation: Infeasibility	-	1.75E-03	1.64E-03	5.90E-06
Simulation: Objective	-	6.03500	5.74218	5.72864

The best known optimal objective value of this problem given is given in Sager 2005<bibref>Sager2005</bibref> by 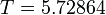$T = 5.72864$ . The corresponding solution is shown in the rightmost plot. The solution of bang-bang type switches five times, starting with $w(t) = 1$ .

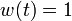Reference solution plots
Optimal relaxed control on a coarse control discretization grid and corresponding differential states.
Optimal relaxed control on a fine, adaptively chosen control discretization grid and corresponding differential states.
Optimal integer control and corresponding differential states.

Source Code

C

The differential equations in C code:

double x1 = xd[0];
double x2 = xd[1];
double x3 = xd[2];
 
double u0 = -0.05236;
double u1 = 0.05236;
double f00, f10, f20;
double f01, f11, f21;
 
f00 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2
      - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u0 + 0.28*x1*x1*u0 + 0.47*x1*u0*u0 + 0.63*u0*u0*u0;
f10 = x3;
f20 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
      - 20.967*u0 + 6.265*x1*x1*u0 + 46*x1*u0*u0 + 61.4*u0*u0*u0;
 
f01 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2
      - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u1 + 0.28*x1*x1*u1 + 0.47*x1*u1*u1 + 0.63*u1*u1*u1;
f11 = x3;
f21 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
      -20.967*u1 + 6.265*x1*x1*u1 + 46*x1*u1*u1 + 61.4*u1*u1*u1;
 
rhs[0] = u[0]*f01 + (1-u[0])*f00;
rhs[1] = u[0]*f11 + (1-u[0])*f10;
rhs[2] = u[0]*f21 + (1-u[0])*f20;

Miscellaneous and Further Reading

See <bibref>Kaya2003</bibref> and <bibref>Sager2005</bibref> for details.

References

@@ Line 66: / Line 66: @@
 | align=center | 1 || align=center | 1 || 0.00000 || 0.10292 || 0.10235
 |-
-| align=center | 2 || align=center | 0 || 2.18000 || 1.92793 || 1.92812
+| align=center | 2 || align=center | 0 || 2.18800 || 1.92793 || 1.92812
 |-
 | align=center | 3 || align=center | 1 || 0.16400 || 0.16687 || 0.16645

Difference between revisions of "F-8 aircraft"

Revision as of 15:52, 8 April 2009

Contents

Mathematical formulation

Reformulation

Reference solutions

Source Code

C

Miscellaneous and Further Reading

References

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Support

Tools