Difference between revisions of "Category:Solution characterization"
From mintOC
m (New page: In this category all sub-categories are listed that describe specific behavior of an optimal solution. Hence, all problems can be identified that share common characteristics, such as an o...) |
m (Initial setup of IMA paper text) |
||
| Line 1: | Line 1: | ||
| − | + | The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle <bibref>Pontryagin1962</bibref> applied here only to the relaxation of the binary control functions <math>\omega(\cdot)</math>, denoted by <math>\alpha(\cdot) \in [0,1]^{n_\omega}</math>. In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, <bibref>Srinivasan2003</bibref>, where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs. | |
| + | |||
| + | Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs. | ||
| + | |||
| + | == References == | ||
| + | <bibreferences/> | ||
[[Category:Problem characterization]] | [[Category:Problem characterization]] | ||
Revision as of 13:19, 20 November 2010
The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle <bibref>Pontryagin1962</bibref> applied here only to the relaxation of the binary control functions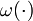 
, denoted by ![\alpha(\cdot) \in [0,1]^{n_\omega}](https://mintoc.de/images/math/6/d/4/6d44af77747bea2951d669a09e98b55d.png)
. In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, <bibref>Srinivasan2003</bibref>, where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs.
Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs.
References
<bibreferences/>
Subcategories
This category has the following 5 subcategories, out of 5 total.
