Goddart's rocket problem
From mintOC
Revision as of 22:06, 27 January 2016 by FelixMueller (Talk | contribs)
| Goddart's rocket problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Continuous control functions: | 1 |
| Path constraints: | 1 |
| Interior point equalities: | 4 |
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.
Contents
[hide]Variables
The state variables 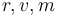 describe the altitude(radius), speed and mass respectively.
describe the altitude(radius), speed and mass respectively.
The drag is given by
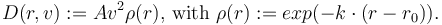
Mathematical formulation
![\begin{array}{llcll}
\displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex]
\mbox{s.t.} & \dot{r}(t) & = & v, \\
& \dot{v}(t) & = & -\frac{1}{r(t)^2} + \frac{1}{m(t)} (T_{max}u(t)-D(r,v)) \\[1.5ex]
& \dot{m}(t) & = & -b T_{max} u(t), \\
& u(t) &\in& [0,1] \\
& r(0) &=& r_0, \\
& v(0) &=& v_0, \\
& m(0) &=& m_0, \\
& r(T) &=& r_T, \\
& D(r(t),v(t))&\le& C \\
& T \, free
\end{array}](https://mintoc.de/images/math/0/3/5/035cf1ae2054bb7adcb297151c972b43.png)
Parameters
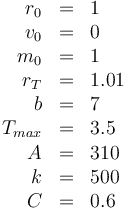
Reference Solution
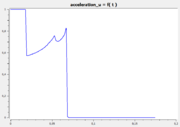
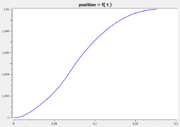
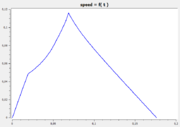
The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389.
- Reference solution plots
Source Code
Model descriptions are available in:
References
The Problem can be found in the BOCOP User Guide.