F-8 aircraft

F-8 aircraft
State dimension:	1
Differential states:	3
Discrete control functions:	1
Interior point equalities:	6

The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by \cite{Kaya2003} and aims at controlling an aircraft in a time--optimal way from an initial state to a terminal state.

The mathematical equations form a small-scale ODE Model. The interior point equality conditions fix both initial and terminal values of the differential states.

The optimal integer control functions shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.

Mathematical formulation

For $t \in [0, T]$ almost everywhere the mixed-integer optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 \\ &&& + 3.846 \; x_0^3 - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ & x(0) &=& x_0, \\ & x(T) &=& x_T, \\ & w(t) &\in& \{-0.05236,0.05236\}. \end{array}$

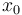$x_0$ is the angle of attack in radians, 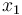$x_1$ is the pitch angle, 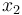$x_2$ is the pitch rate in rad/s, and the control function 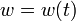$w = w(t)$ is the tail deflection angle in radians. This model goes back to \cite{Garrard1977}. See \cite{Kaya2003} for further references and details.

Initial and terminal values

Both initial as terminal values of the differential states are fixed.

$\begin{array}{rcl} x_0 &=& (0.4655,0,0)^T, \\ x_T &=& (0,0,0)^T. \end{array}$

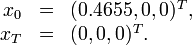
Reference solutions

If the problem is relaxed, i.e., we demand that 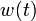$w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$,

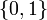The optimal objective value of this relaxed problem is 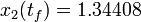$x_2(t_f) = 1.34408$. As follows from MIOC theory<bibref>Sager2008</bibref> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of 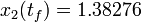$x_2(t_f) = 1.38276$, and one with 56 switches and $x_2(t_f) = 1.34416$.

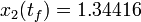• Reference solution plots
• 

  Optimal relaxed control determined by an indirect approach and by a direct approach on different control discretization grids.

• 

  Differential states and corresponding adjoint variables in the indirect approach.

• 

  Control and differential states with only two switches.

• 

  Control and differential states with 56 switches.

Source Code

C

The differential equations in C code:

Miscellaneous and Further Reading

See <bibref>Kaya2003</bibref> and <bibref>Sager2005</bibref> for details.

References

<bibreferences/>