Lotka Volterra fishing problem (Casadi)

This page contains a discretized version of the MIOCP Lotka Volterra fishing problem in Casadi format.

Casadi

The model in Python code for a fixed control discretization grid using direct multiple shooting.

# ------------------------------------------------------------------------------
# Lotka Volterra fishing problem with CasADi Python interface using direct
# multiple shooting with IPOPT and Sundials' integrator CVodes
#
# NOTE: CasADi currently has no support for mixed-integer problems. Only the
# relaxed solution is calculated
# ------------------------------------------------------------------------------
 
# Import
from casadi import *
 
# Introduce model parameters
t0 =  0
tf = 12
c0 =  0.4
c1 =  0.2
x0 = [0.5, 0.7, 0]
 
# Define length of time horizon as well as number and length of intervals
T  = tf - t0
N  = 100
dt = float(T) / N
 
# Define the DAE
x = SX.sym('x', 3)
w = SX.sym('w')
rhs = vertcat([
    dt * ( x[0] - x[0] * x[1] - c0 * x[0] * w),
    dt * (-x[1] + x[0] * x[1] - c1 * x[1] * w),
    dt * ((x[0] - 1)**2 + (x[1] - 1)**2)
])
dae = SXFunction("dae", daeIn(x=x, p=w), daeOut(ode=rhs))
 
I_opt = {
    'linear_solver': 'csparse',
    't0':             0.0,
    'tf':             1.0
}
I = Integrator("integrate", "cvodes", dae, I_opt)
 
# Define number of state variables, controls and variables per interval
nx = x.size1()  # Number of states
nu = w.size1()  # Number of controls
ns = nx + nu    # Number of variables per shooting interval
 
# Create symbolic expressions for actual NLP variables and define DMS structure
X = MX.sym('X', (N + 1) * nx + N * nu)            # Optimization variables
G = []                                            # Nonlinear constraints
F = X[N*ns+2]                                     # Mayer objective
for i in range(0, N):
    X0 = X[i*ns:i*ns+nx]                          # Initial state for interval
    U  = X[i*ns+nx:(i+1)*ns]                      # Control for interval
    X1 = X[(i+1)*ns:(i+1)*ns+nx]                  # Terminal state for interval
 
    Y = I({'x0': X0, 'p': U})
    G = vertcat([G, Y['xf'] - X1])
 
# Define NLP
nlp = MXFunction('nlp', nlpIn(x=X), nlpOut(f=F, g=G))
 
# Create feasible initial solution by simulating with constant zero control
Xstart = DMatrix.zeros(X.size1(), X.size2())
Xstart[0:nx] = x0
for i in range(0, N):
    X0 = Xstart[i*ns:i*ns+nx]
    Xstart[i*ns+nx:(i+1)*ns]     = 0.0
    Xstart[(i+1)*ns:(i+1)*ns+nx] = I({'x0': X0, 'p': 0.0})['xf']
 
# Create and execute nonlinear solver
solver = NlpSolver('solver', 'ipopt', nlp)
result = solver({
    'x0':  Xstart,
    'lbg': DMatrix.zeros(G.size1()),
    'ubg': DMatrix.zeros(G.size1()),
    'lbx': x0 + [0.0] + [0.0, 0.0, 0.0, 0.0] * (N - 1) + [0.0, 0.0, 0.0],
    'ubx': x0 + [1.0] + [inf, inf, inf, 1.0] * (N - 1) + [inf, inf, inf]
})
 
# Extract solution and objective
x = result['x']
f = result['f']
 
# Disassemble solution into easily plottable lists
t  = [i*dt       for i in range(0, N + 1)]
x0 = [x[i*ns]    for i in range(0, N + 1)]
x1 = [x[i*ns+1]  for i in range(0, N + 1)]
u  = [x[i*ns+nx] for i in range(0, N    )]

Results

IPOPT

The relaxed solution calculated by IPOPT (Ipopt 3.12, Linux x86_64, default settings, 4 GHz quadcore, Linux 4.2.0-23-generic) has an objective function value of 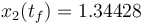$x_2(t_f) = 1.34428$. IPOPT requires 22 iterations (6.062 seconds of processing time). The following is a Gnuplot compatible tabular version of the solution:

#         t,         x_0,         x_1,           u
          0,         0.5,         0.7, 5.18436e-09
       0.12,    0.519594,    0.659989, 5.42459e-09
       0.24,    0.542429,    0.623852, 5.79496e-09
       0.36,    0.568601,    0.591429, 6.30563e-09
       0.48,     0.59823,    0.562571, 6.97415e-09
        0.6,    0.631456,    0.537143,   7.827e-09
       0.72,     0.66843,    0.515028, 8.90236e-09
       0.84,    0.709312,    0.496134, 1.02545e-08
       0.96,     0.75426,    0.480401, 1.19611e-08
       1.08,    0.803421,      0.4678, 1.41346e-08
        1.2,    0.856919,    0.458344, 1.69417e-08
       1.32,    0.914842,    0.452091, 2.06377e-08
       1.44,     0.97722,    0.449154, 2.56285e-08
       1.56,       1.044,    0.449708,  3.2592e-08
       1.68,     1.11503,    0.454003, 4.27322e-08
        1.8,     1.18998,    0.462372, 5.83658e-08
       1.92,     1.26837,    0.475251, 8.44574e-08
       2.04,     1.34942,    0.493189, 1.33425e-07
       2.16,     1.43209,    0.516862, 2.44977e-07
       2.28,     1.51492,    0.547087, 6.24464e-07
        2.4,     1.59605,    0.584816,    0.715281
       2.52,     1.61776,     0.61833,    0.999999
       2.64,     1.61116,      0.6499,    0.999999
       2.76,     1.59844,     0.68229,           1
       2.88,     1.57963,    0.714939,           1
          3,     1.55497,    0.747196,           1
       3.12,     1.52487,    0.778343,    0.999999
       3.24,     1.48993,    0.807625,    0.999999
       3.36,      1.4509,     0.83429,    0.999999
       3.48,     1.40865,    0.857635,    0.999998
        3.6,     1.36412,    0.877047,    0.999997
       3.72,     1.31827,    0.892039,    0.999991
       3.84,     1.27203,     0.90228,    0.999646
       3.96,     1.22628,    0.907616,    0.536112
       4.08,     1.20755,    0.919653,    0.581667
        4.2,     1.18502,    0.928525,    0.503883
       4.32,     1.16606,    0.936899,    0.464153
       4.44,     1.14851,    0.944178,    0.418428
       4.56,     1.13278,    0.950658,    0.378617
       4.68,     1.11859,    0.956378,    0.341493
        4.8,     1.10582,    0.961433,      0.3073
       4.92,     1.09438,    0.965904,    0.276462
       5.04,     1.08411,    0.969849,    0.248219
       5.16,     1.07492,    0.973333,    0.222481
       5.28,      1.0667,    0.976412,     0.19935
        5.4,     1.05936,     0.97913,    0.178262
       5.52,      1.0528,    0.981533,    0.159402
       5.64,     1.04696,    0.983656,    0.142349
       5.76,     1.04175,    0.985532,    0.127041
       5.88,      1.0371,    0.987191,      0.1133
          6,     1.03297,    0.988657,    0.100985
       6.12,     1.02929,    0.989954,   0.0899604
       6.24,     1.02601,    0.991101,   0.0800981
       6.36,      1.0231,    0.992117,   0.0712934
       6.48,     1.02051,    0.993015,   0.0634308
        6.6,     1.01821,    0.993811,   0.0564127
       6.72,     1.01617,    0.994515,   0.0501573
       6.84,     1.01435,    0.995139,   0.0445824
       6.96,     1.01274,    0.995691,   0.0396177
       7.08,     1.01131,     0.99618,   0.0351979
        7.2,     1.01003,    0.996613,   0.0312714
       7.32,      1.0089,    0.996997,    0.027765
       7.44,      1.0079,    0.997337,   0.0246626
       7.56,     1.00701,    0.997639,   0.0218975
       7.68,     1.00622,    0.997905,   0.0194423
        7.8,     1.00552,    0.998142,   0.0172603
       7.92,      1.0049,    0.998351,   0.0153224
       8.04,     1.00435,    0.998537,   0.0136015
       8.16,     1.00386,    0.998701,   0.0120735
       8.28,     1.00342,    0.998847,   0.0107171
        8.4,     1.00303,    0.998976,  0.00951328
       8.52,     1.00269,     0.99909,  0.00844491
       8.64,     1.00239,    0.999191,  0.00749702
       8.76,     1.00212,    0.999281,  0.00665598
       8.88,     1.00188,     0.99936,  0.00590975
          9,     1.00167,     0.99943,  0.00524776
       9.12,     1.00148,    0.999492,  0.00466052
       9.24,     1.00131,    0.999547,  0.00413914
       9.36,     1.00117,    0.999596,  0.00367206
       9.48,     1.00103,    0.999637,  0.00326159
        9.6,     1.00092,    0.999675,  0.00290302
       9.72,     1.00082,    0.999707,  0.00258504
       9.84,     1.00072,    0.999736,  0.00230262
       9.96,     1.00064,    0.999762,  0.00205186
      10.08,     1.00057,    0.999785,  0.00182951
       10.2,     1.00051,    0.999805,  0.00163302
      10.32,     1.00045,    0.999822,  0.00146039
      10.44,      1.0004,    0.999838,  0.00131011
      10.56,     1.00036,    0.999851,  0.00118097
      10.68,     1.00032,    0.999863,  0.00107188
       10.8,     1.00028,    0.999872, 0.000981659
      10.92,     1.00025,     0.99988,  0.00090944
      11.04,     1.00022,    0.999886, 0.000854893
      11.16,     1.00019,     0.99989, 0.000818284
      11.28,     1.00017,    0.999892, 0.000801181
       11.4,     1.00014,    0.999891, 0.000807844
      11.52,     1.00012,    0.999886, 0.000848734
      11.64,     1.00009,    0.999878, 0.000951928
      11.76,     1.00006,    0.999864,  0.00121852
      11.88,     1.00002,    0.999838,  0.00267036
         12,    0.999915,    0.999769,           0