Category:Solution characterization

The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle [Pontryagin1962]Address: Chichester
Author: Pontryagin, L.S.; Boltyanski, V.G.; Gamkrelidze, R.V.; Miscenko, E.F.
Publisher: Wiley
Title: The Mathematical Theory of Optimal Processes
Year: 1962
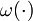applied here only to the relaxation of the binary control functions , denoted by . In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, [Srinivasan2003]Author: Srinivasan, B.; Palanki, S.; Bonvin, D.
Journal: Computers \& Chemical Engineering
Pages: 1--26
Title: Dynamic Optimization of Batch Processes: I. Characterization of the Nominal Solution
Volume: 27
Year: 2003
, where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs.

Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs.

References

[Pontryagin1962]	Pontryagin, L.S.; Boltyanski, V.G.; Gamkrelidze, R.V.; Miscenko, E.F. (1962): The Mathematical Theory of Optimal Processes. (%edition%). Wiley, Chichester, %pages%
[Srinivasan2003]	Srinivasan, B.; Palanki, S.; Bonvin, D. (2003): Dynamic Optimization of Batch Processes: I. Characterization of the Nominal Solution. Computers \& Chemical Engineering, 27, 1--26