Hanging chain problem

Hanging chain problem
State dimension:	1
Differential states:	2
Discrete control functions:	1
Interior point equalities:	2

The Hanging chain problem is concerned with finding a chain (of uniform density) of length 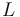$L$ suspendend between two points 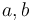$a, b$ with minimal potential energy. (Problem taken from the COPS library)

Mathematical formulation

The problem is given by

Failed to parse (syntax error): \begin{array}{llcl} \displaystyle \min_{x, u} &x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = & u, \\ & \dot{x}_2 & = & x_1 (1+u^2)^{1/2}, \\ & \dot{x}_3 & = & (1+u^2)^{1/2), \\ & x(t_0) &=& (a,0,0)^T, \\ & x_1(t_f) &=& b, \\ & x_3(t_f) &=& Lp, \\ & x(t) &\in& [0,10], \\ & u(t) &\in& [-10,20]. \end{array}

Parameters

In this model the parameters used are \begin{array}{rcl} [t_0, t_f] &=& [0, 1],\\ (a,b) &=& (0.4, 0.2),\\ Lp &=& 4. \end{array}

Source Code

Model descriptions are available in

• AMPL/TACO code at Hanging chain problem (TACO)