Egerstedt standard problem

Egerstedt standard problem
State dimension:	1
Differential states:	3
Discrete control functions:	3
Path constraints:	1
Interior point equalities:	3

The Egerstedt standard problemm is the problem is of an academic nature and was proposed by Egerestedt to highlight the features of an Hybrid System algorithm in 2006 [Egerstedt2006]Author: M. Egerstedt; Y. Wardi; H. Axelsson
Journal: IEEE Transactions on Automatic Control
Pages: 110--115
Title: Transition-time optimization for switched-mode dynamical systems
Volume: 51
Year: 2006
. It has been used since then in many MIOCP research studies (e.g. [Jung2013]Author: M. Jung; C. Kirches; S. Sager
Booktitle: Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschel
Editor: M. J\"unger and G. Reinelt
Pages: 387--417
Publisher: Springer Berlin Heidelberg
Title: On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control
Url: http://www.mathopt.de/PUBLICATIONS/Jung2013.pdf
Year: 2013
) for benchmarking of MIOCP algorithms.

Mathematical formulation

The mixed-integer optimal control problem after partial outer convexification is given by

$\begin{array}{llclr} \displaystyle \min_{x, \omega} & x_3(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = & -x_1\omega_1 + (x_1+x_2)\omega_2+(x_1-x_2)\omega_3, \\ & \dot{x}_2 & = & (x_1+2x_2)\omega_1+(x_1-2x_2)\omega_2+(x_1+x_2)\omega_3, \\ & \dot{x}_3 & = & x_1^2+x_2^2, \\[1.5ex] & x(0) &=& (0.5, 0.5, 0)^T, \\ & x_2(t) & \geq & 0.4, \\ & 1 &=& \sum\limits_{i=1}^3\omega_i(t), \\ & \omega(t) &\in& \{0, 1\}, \end{array}$

for $t \in [t_0, t_f]=[0,1]$.

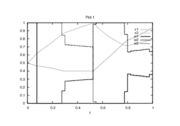
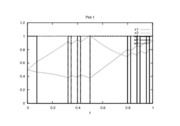
Reference Solutions

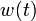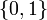If the problem is relaxed, i.e., we demand that $w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$, the optimal solution can be determined by using a direct method such as collocation or Bock's direct multiple shooting method.

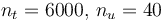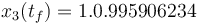The optimal objective value of the relaxed problem with $n_t=6000, \, n_u=40$ is $x_3(t_f)=1.0.995906234$. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 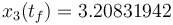$x_3(t_f) =3.20831942$. The binary control solution was evaluated in the MIOCP by using a Merit function with additional Lagrange term $100 \max\limits_{t\in[0,1]}\{0,0.4-x_2(t)\}$.

• Reference solution plots
• 

  Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and $n_t=6000, \, n_u=40$.

• 

  Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and $n_t=6000, \, n_u=40$. The relaxed controls were approximated by Combinatorial Integral Approximation.

Source Code

Model descriptions are available in

• AMPL code at Lotka Volterra fishing problem (AMPL)

References

[Egerstedt2006]	M. Egerstedt; Y. Wardi; H. Axelsson (2006): Transition-time optimization for switched-mode dynamical systems. IEEE Transactions on Automatic Control, 51, 110--115
[Jung2013]	M. Jung; C. Kirches; S. Sager (2013): On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control. Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschel

We present numerical results for a benchmark MIOCP from a previous study [157] with the addition of switching constraints. In its original form, the problem was:

After partial outer convexification with respect to the integer control v, the binary convexified counterpart problem reads