D'Onofrio model (binary variant)

D'Onofrio model (binary variant)
State dimension:	1
Differential states:	4
Discrete control functions:	4
Path constraints:	2

This site describes a D'Onofrio model variant with four binary controls instead which of only two continuous controls. The continuous controls are replaced via the outer convexifacation method.

Mathematical formulation

For $t \in [t_0, t_f]$ the optimal control problem is given by

Failed to parse (PNG conversion failed; check for correct installation of latex and dvipng (or dvips + gs + convert)): {\begin{array}{llcl}\displaystyle \min _{{x,u}}&x_{0}(t_{f})&+&\alpha \int _{{t_{0}}}^{{t_{f}}}u_{0}(t)^{2}{\text{d}}t\\[1.5ex]{\mbox{s.t.}}&{\dot {x}}_{0}&=&-\zeta x_{0}{\text{ln}}\left({\frac {x_{0}}{x_{1}}}\right)-\sum \limits _{{i=1}}^{{4}}w_{i}\;c_{{1,i}}\;F\;x_{0},\\&{\dot {x}}_{1}&=&bx_{0}-\mu x_{1}-dx_{0}^{{{\frac {2}{3}}}}x_{1}-\sum \limits _{{i=1}}^{{4}}w_{i}c_{{0,i}}Gx_{1}-\sum \limits _{{i=1}}^{{4}}w_{i}\;c_{{1,i}}\eta x_{1},\\&{\dot {x}}_{2}&=&\sum \limits _{{i=1}}^{{4}}w_{i}\;c_{{0,i}},\\&{\dot {x}}_{3}&=&\sum \limits _{{i=1}}^{{4}}w_{i}\;c_{{1,i}},\\[1.5ex]&x_{2}&\leq &x_{2}^{{max}},\\&x_{3}&\leq &x_{3}^{{max}},&1&=&\sum \limits _{{i=1}}^{{3}}w_{i}(t),\\&w_{i}(t)&\in &\{0,1\},\quad i=1\ldots 4.\end{array}}

Parameters

These fixed values are used within the model:

$[t_0,t_f]=[0,20], c_1=-1, c_2=0.75, c_3=-2.$

Reference Solutions

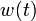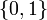If the problem is relaxed, i.e., we demand that $w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$, the optimal solution can be determined by means of direct optimal control.

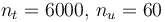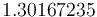The optimal objective value of the relaxed problem with $n_t=6000, \, n_u=60$ is $1.30167235$. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is $1.30273681$.

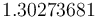• Reference solution plots
• 

  Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and $n_t=6000, \, n_u=60$.

• 

  Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and $n_t=6000, \, n_u=60$. The relaxed controls were approximated by Combinatorial Integral Approximation.

Source Code

Model description is available in

• AMPL code at Van der Pol Oscillator binary variant(AMPL)