Car testdrive (elliptic track)

Car testdrive (elliptic track)
State dimension:	1
Differential states:	7
Continuous control functions:	3
Discrete control functions:	1
Path constraints:	1
Interior point inequalities:	7

The elliptic track testdrive problem is a time optimal periodic control problem with gear shift, first introduced in [Sager2009a]The entry doesn't exist yet..

Mathematical formulation

The mathematical equations form a small-scale ODE model as presented for the lane change manoeuvre.

The vehicle dynamics are based on a single-track model, derived under the simplifying assumption that rolling and pitching of the car body can be neglected. Consequentially, only a single front and rear wheel is modeled, located in the virtual center of the original two wheels. Motion of the car body is considered on the horizontal plane only.

Four controls represent the driver's choice on steering and velocity. We denote with 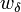$w_\delta$ the steering wheel's angular velocity. The force 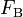$F_\text{B}$ controls the total braking force, while the accelerator pedal position 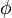$\phi$ is translated into an accelerating force. Finally, the selected gear 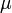$\mu$ influences the effective engine torque's transmission.

Resulting MIOCP

For $t \in [t_0, t_f]$ almost everywhere the mixed-integer optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x(\cdot), u(\cdot), \mu(\cdot)} & t_\text{f} \\[1.5ex] \mbox{s.t.} & \dot{x} & = & f(t, x, u, \mu), \\ & c_\text{x}(t_0) &=& c_\text{x}(t_f), \\ & c_\text{y}(t_0) &=& c_\text{y}(t_f), \\ & v(t_0) &=& v(t_f), \\ & \beta(t_0) &=& \beta(t_f) - 2\pi, \\ & \psi(t_0) &=& \psi(t_f), \\ & \delta(t_0) &=& \delta(t_f), \\ & r(t,x,u) &\geq& 0, \\ & \mu(t) &\in& \{1, 2, 3, 4, 5\}. \end{array}$

Variants

See testdrive overview page.

References

[Sager2009a]

The entry doesn't exist yet.