Category:Outer convexification
For time-dependent and space- independent integer controls often another formulation is beneficial, e.g., [Kirches2010]Author: C. Kirches; S. Sager; H.G. Bock; J.P. Schl\"oder
Journal: Optimal Control Applications and Methods
Month: March/April
Number: 2
Pages: 137--153
Title: Time-optimal control of automobile test drives with gear shifts
Url: http://mathopt.de/PUBLICATIONS/Kirches2010.pdf
Volume: 31
Year: 2010 . For every element
. For every element 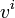 of
of 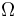 a binary control function
a binary control function 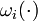 is introduced.
is introduced.
The general equation
![0 = F[x,u,v(t)]](https://mintoc.de/images/math/d/a/6/da6a3ccbfc2da9b4587a746c69806413.png)
can then be written as
![0 = \sum_{i=1}^{n_{\omega}} F[x,u,v^i] \; \omega_i (t), \;\;\;\; t \in [0, t_f].](https://mintoc.de/images/math/a/1/8/a1806642fed3c7bf47027381e6d65a46.png)
If we impose the special ordered set type one condition
![\sum_{i=1}^{n_{\omega}} \omega_i (t) = 1, \;\;\;\; t \in [0, t_f],](https://mintoc.de/images/math/0/3/7/037a055b49541ba5af17b1339bd92068.png)
there is a bijection between every feasible integer function 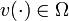 and an appropriately chosen binary function
and an appropriately chosen binary function 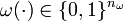 , compare [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
, compare [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
Journal: Mathematical Programming
Number: 1
Pages: 109--149
Title: Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems
Url: http://mathopt.de/PUBLICATIONS/Sager2009.pdf
Volume: 118
Year: 2009 . The relaxation of
. The relaxation of 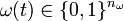 is given by
is given by ![\omega(t) \in [0,1]^{n_{\omega}}](https://mintoc.de/images/math/d/5/7/d574a9fce802239a6bb374d6011b4646.png) . We will refer to the two constraints as outer convexification [Sager2005]Address: Tönning, Lübeck, Marburg
. We will refer to the two constraints as outer convexification [Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005 of the original model.
of the original model.
References
| [Kirches2010] | C. Kirches; S. Sager; H.G. Bock; J.P. Schl\"oder (2010): Time-optimal control of automobile test drives with gear shifts. Optimal Control Applications and Methods, 31, 137--153 |  |
| [Sager2005] | S. Sager (2005): Numerical methods for mixed--integer optimal control problems. (%edition%). Der andere Verlag, Tönning, Lübeck, Marburg, %pages% |  |
| [Sager2009] | Sager, S.; Reinelt, G.; Bock, H.G. (2009): Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems. Mathematical Programming, 118, 109--149 |  |
Pages in category "Outer convexification"
This category contains only the following page.