Difference between revisions of "Egerstedt standard problem"

From mintOC
Jump to: navigation, search
m (Fixed type, error in relaxed objective function value)
 
(3 intermediate revisions by one other user not shown)
Line 7: Line 7:
 
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout...
 
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout...
  
−
-->The '''Egerstedt standard problemm''' is the problem is of an academic nature and was proposed by Egerestedt to highlight the features of an Hybrid System algorithm in 2006 <bib id="Egerstedt2006" />. It has been used since then in many MIOCP research studies (e.g. <bib id="Jung2013" />) for benchmarking of MIOCP algorithms.
+
-->The '''Egerstedt standard problem''' is the problem is of an academic nature and was proposed by Egerestedt to highlight the features of an Hybrid System algorithm in 2006 <bib id="Egerstedt2006" />. It has been used since then in many MIOCP research studies (e.g. <bib id="Jung2013" />) for benchmarking of MIOCP algorithms.
  
  
Line 28: Line 28:
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
−
for <math>t \in [t_0, t_f]=[0,1] </math>.
 
 
</p>
 
</p>
 +
for <math>t \in [t_0, t_f]=[0,1] </math>.
  
 
== Reference Solutions ==
 
== Reference Solutions ==
  
−
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of [http://en.wikipedia.org/wiki/Pontryagin%27s_minimum_principle Pontryagins maximum principle]. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.
+
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by using a direct method such as collocation or Bock's direct multiple shooting method.  
  
−
The optimal objective value of this relaxed problem is <math>x_2(t_f) = 1.34408</math>. As follows from MIOC theory <bib id="Sager2011d" /> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of <math>x_2(t_f) = 1.38276</math>, and one with 56 switches and <math>x_2(t_f) = 1.34416</math>.
+
The optimal objective value of the relaxed problem with  <math> n_t=6000, \, n_u=40  </math> is <math>x_3(t_f)=0.995906234</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>x_3(t_f) =3.20831942</math>.  The binary control solution was evaluated in the MIOCP by using a Merit function with additional Lagrange term <math> 100 \max\limits_{t\in[0,1]}\{0,0.4-x_2(t)\}  </math>.
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
−
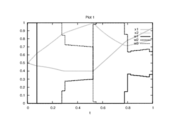
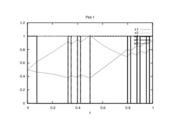
  Image:lotkaRelaxedControls.png| Optimal relaxed control determined by an indirect approach and by a direct approach on different control discretization grids.
+
  Image:EgerstedtRelaxed 6000 150 1.png| Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and <math>n_t=6000, \, n_u=40</math>.
−
  Image:lotkaindirektStates.png| Differential states and corresponding adjoint variables in the indirect approach.
+
  Image:EgerstedtCIA 6000 150 1.png| Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=6000, \, n_u=40</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
−
  Image:lotka2Switches.png| Control and differential states with only two switches.
+
−
Image:lotka56Switches.png| Control and differential states with 56 switches.
+
 
</gallery>
 
</gallery>
 +
  
  
 
== Source Code ==
 
== Source Code ==
  
−
Model descriptions are available in
+
Model description is available in
 +
* [[:Category:AMPL | AMPL code]] at [[Egerstedt standard problem (AMPL)]]
  
−
* [[:Category:ACADO | ACADO code]] at [[Lotka Volterra fishing problem (ACADO)]]
 
−
* [[:Category:AMPL | AMPL code]] at [[Lotka Volterra fishing problem (AMPL)]]
 
−
* [[:Category:APMonitor | APMonitor code]] at [[Lotka Volterra fishing problem (APMonitor)]]
 
−
* [[:Category:Bocop | Bocop code]] at [[Lotka Volterra fishing problem (Bocop)]]
 
−
* [[:Category:Casadi | Casadi code]] at [[Lotka Volterra fishing problem (Casadi)]]
 
−
* [[:Category:JModelica | JModelica code]] at [[Lotka Volterra fishing problem (JModelica)]]
 
−
* [[:Category:Julia/JuMP | JuMP code]] at [[Lotka Volterra fishing problem (JuMP)]]
 
−
* [[:Category:Muscod | Muscod code]] at [[Lotka Volterra fishing problem (Muscod)]]
 
−
* [[:Category:switch | switch code]] at [[Lotka Volterra fishing problem (switch)]]
 
−
* [[:Category:TomDyn/PROPT | PROPT code]] at [[Lotka Volterra fishing problem (TomDyn/PROPT)]]
 
  
−
== Variants ==
 
−
 
−
There are several alternative formulations and variants of the above problem, in particular
 
−
 
−
* a prescribed time grid for the control function <bib id="Sager2006" />, see also [[Lotka Volterra fishing problem (AMPL)]],
 
−
* a time-optimal formulation to get into a steady-state <bib id="Sager2005" />,
 
−
* the usage of a different target steady-state, as the one corresponding to <math> w(t) = 1</math> which is <math>(1 + c_1, 1 - c_0)</math>, see [[Lotka Volterra multi-arcs problem]]
 
−
* different fishing control functions for the two species, see [[Lotka Volterra Multimode fishing problem]]
 
−
* different parameters and start values.
 
−
 
−
== Miscellaneous and Further Reading ==
 
−
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bib id="Sager2006" /> and revisited in his PhD thesis <bib id="Sager2005" />. These are also the references to look for more details.
 
  
 
== References ==
 
== References ==
Line 80: Line 58:
 
[[Category:ODE model]]
 
[[Category:ODE model]]
 
[[Category:Tracking objective]]
 
[[Category:Tracking objective]]
−
[[Category:Chattering]]
 
 
[[Category:Sensitivity-seeking arcs]]
 
[[Category:Sensitivity-seeking arcs]]
−
[[Category:Population dynamics]]
+
 
  
  

Latest revision as of 17:09, 19 September 2019

Egerstedt standard problem
State dimension: 1
Differential states: 3
Discrete control functions: 3
Path constraints: 1
Interior point equalities: 3

The Egerstedt standard problem is the problem is of an academic nature and was proposed by Egerestedt to highlight the features of an Hybrid System algorithm in 2006 [Egerstedt2006]Author: M. Egerstedt; Y. Wardi; H. Axelsson
Journal: IEEE Transactions on Automatic Control
Pages: 110--115
Title: Transition-time optimization for switched-mode dynamical systems
Volume: 51
Year: 2006
Link to Google Scholar. It has been used since then in many MIOCP research studies (e.g. [Jung2013]Author: M. Jung; C. Kirches; S. Sager
Booktitle: Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschel
Editor: M. J\"unger and G. Reinelt
Pages: 387--417
Publisher: Springer Berlin Heidelberg
Title: On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control
Url: http://www.mathopt.de/PUBLICATIONS/Jung2013.pdf
Year: 2013
Link to Google Scholar) for benchmarking of MIOCP algorithms.


Mathematical formulation

The mixed-integer optimal control problem after partial outer convexification is given by

\begin{array}{llclr} \displaystyle \min_{x, \omega} & x_3(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = & -x_1\omega_1 + (x_1+x_2)\omega_2+(x_1-x_2)\omega_3, \\ & \dot{x}_2 & = & (x_1+2x_2)\omega_1+(x_1-2x_2)\omega_2+(x_1+x_2)\omega_3, \\ & \dot{x}_3 & = & x_1^2+x_2^2, \\[1.5ex] & x(0) &=& (0.5, 0.5, 0)^T, \\ & x_2(t) & \geq & 0.4, \\ & 1 &=& \sum\limits_{i=1}^3\omega_i(t), \\ & \omega(t) &\in& \{0, 1\}, \end{array}

for t \in [t_0, t_f]=[0,1] .

Reference Solutions

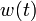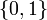If the problem is relaxed, i.e., we demand that w(t) be in the continuous interval [0, 1] instead of the binary choice \{0,1\}, the optimal solution can be determined by using a direct method such as collocation or Bock's direct multiple shooting method.

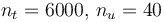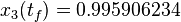The optimal objective value of the relaxed problem with n_t=6000, \, n_u=40 is x_3(t_f)=0.995906234. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 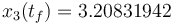x_3(t_f) =3.20831942. The binary control solution was evaluated in the MIOCP by using a Merit function with additional Lagrange term 100 \max\limits_{t\in[0,1]}\{0,0.4-x_2(t)\} .

  • Reference solution plots

  • Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and n_t=6000, \, n_u=40.

  • Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and n_t=6000, \, n_u=40. The relaxed controls were approximated by Combinatorial Integral Approximation.


Source Code

Model description is available in


References

[Egerstedt2006]M. Egerstedt; Y. Wardi; H. Axelsson (2006): Transition-time optimization for switched-mode dynamical systems. IEEE Transactions on Automatic Control, 51, 110--115Link to Google Scholar
[Jung2013]M. Jung; C. Kirches; S. Sager (2013): On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control. Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschelLink to Google Scholar
[Sager2005]S. Sager (2005): Numerical methods for mixed--integer optimal control problems. (%edition%). Der andere Verlag, Tönning, Lübeck, Marburg, %pages%Link to Google Scholar
[Sager2006]S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder (2009): Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem. Springer, Recent Advances in OptimizationLink to Google Scholar
[Sager2011d]S. Sager: On the Integration of Optimization Approaches for Mixed-Integer Nonlinear Optimal Control, 2011Link to Google Scholar




We present numerical results for a benchmark MIOCP from a previous study [157] with the addition of switching constraints. In its original form, the problem was:


After partial outer convexification with respect to the integer control v, the binary convexified counterpart problem reads

Retrieved from "https://mintoc.de/index.php?title=Egerstedt_standard_problem&oldid=2305"