Difference between revisions of "F-8 aircraft"

From mintOC
Jump to: navigation, search
m
m (Added plots)
Line 46: Line 46:
 
== Reference solutions ==
 
== Reference solutions ==
  
−
The optimal objective value of this  problem given in Sager 2005<bibref>Sager2005</bibref> is <math>T = 5.73406</math>.  
+
The optimal objective value of this  problem given in Sager 2005<bibref>Sager2005</bibref> is <math>T = 5.73406</math>. An even better solution is <math>T = 5.72865</math> that corresponds to the rightmost plot.
  
−
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="3">
+
<gallery caption="Reference solution plots" widths="240px" heights="167px" perrow="3">
−
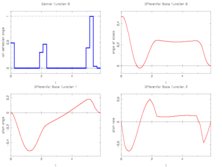
  Image:lotkaRelaxedControls.png| Optimal relaxed control on a coarse control discretization grid and corresponding differential states.
+
  Image:f8aircraftRelaxedCoarse.png| Optimal relaxed control on a coarse control discretization grid and corresponding differential states.
−
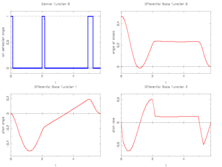
  Image:lotkaindirektStates.png| Optimal relaxed control on a fine control discretization grid and corresponding differential states.
+
  Image:f8aircraftRelaxedFine.png| Optimal relaxed control on a fine, adaptively chosen control discretization grid and corresponding differential states.
−
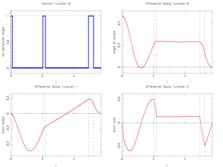
  Image:lotka2Switches.png| Optimal integer control and corresponding differential states.
+
  Image:f8aircraftInteger.png| Optimal integer control and corresponding differential states.
 
</gallery>
 
</gallery>
  

Revision as of 02:03, 1 November 2008

F-8 aircraft
State dimension: 1
Differential states: 3
Discrete control functions: 1
Interior point equalities: 6


The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by Kaya and Noakes in 2003<bibref>Kaya2003</bibref> and aims at controlling an aircraft in a time-optimal way from an initial state to a terminal state.

The mathematical equations form a small-scale ODE Model. The interior point equality conditions fix both initial and terminal values of the differential states.

The optimal integer control functions shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.

Mathematical formulation

For t \in [0, T] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 \\ &&& + 3.846 \; x_0^3 - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ & x(0) &=& x_0, \\ & x(T) &=& x_T, \\ & w(t) &\in& \{-0.05236,0.05236\}. \end{array}

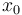x_0 is the angle of attack in radians, 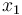x_1 is the pitch angle, 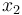x_2 is the pitch rate in rad/s, and the control function 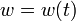w = w(t) is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>.

The control w(t) is restricted to take values from a finite set only. However, as w(t) enters

Initial and terminal values

Both initial as terminal values of the differential states are fixed.

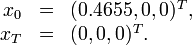
\begin{array}{rcl} x_0 &=& (0.4655,0,0)^T, \\ x_T &=& (0,0,0)^T. \end{array}

Reference solutions

The optimal objective value of this problem given in Sager 2005<bibref>Sager2005</bibref> is 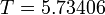T = 5.73406. An even better solution is 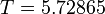T = 5.72865 that corresponds to the rightmost plot.

  • Reference solution plots

  • Optimal relaxed control on a coarse control discretization grid and corresponding differential states.

  • Optimal relaxed control on a fine, adaptively chosen control discretization grid and corresponding differential states.

  • Optimal integer control and corresponding differential states.

Source Code

C

The differential equations in C code: 

double x1 = xd[0];
double x2 = xd[1];
double x3 = xd[2];
 
double u0 = -0.05236;
double u1 = 0.05236;
double f00, f10, f20;
double f01, f11, f21;
 
f00 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2
      - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u0 + 0.28*x1*x1*u0 + 0.47*x1*u0*u0 + 0.63*u0*u0*u0;
f10 = x3;
f20 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
      - 20.967*u0 + 6.265*x1*x1*u0 + 46*x1*u0*u0 + 61.4*u0*u0*u0;
 
f01 = - 0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2
      - x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u1 + 0.28*x1*x1*u1 + 0.47*x1*u1*u1 + 0.63*u1*u1*u1;
f11 = x3;
f21 = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
      -20.967*u1 + 6.265*x1*x1*u1 + 46*x1*u1*u1 + 61.4*u1*u1*u1;
 
rhs[0] = u[0]*f01 + (1-u[0])*f00;
rhs[1] = u[0]*f11 + (1-u[0])*f10;
rhs[2] = u[0]*f21 + (1-u[0])*f20;

Miscellaneous and Further Reading

See <bibref>Kaya2003</bibref> and <bibref>Sager2005</bibref> for details.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=F-8_aircraft&oldid=176"